2.3. Интерполяционная формула Гаусса

В случае квадратичной интерполяции (n=2) вычисление значения функции в некоторой точке X, С заданной точностью ε, предполагает использование трех ближайших к X Узлов. Пусть h = x j – x j-1 - шаг сетки узлов интерполирования, - значения функции в узлах сетки.

Обозначим за Xj ближайший узел к данной точке X.

Обозначим 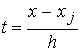и конечные разности первого и второго порядка:

;

.

Тогда интерполяционная формула Гаусса запишется в виде:

F(X)=L2(X)=,

Где R2(X)=f(X)-L2(X) – Остаточный член, вычисляемый по формуле:

R2 (X) = 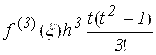, где x Î [Xj-1, Xj+1].

Шаг H Выбирается из условия | R2 (X) | ≤ ε

< Предыдущая		Следующая >