9.2.4. Пример выполнения задачи 3

Задача. Минимизировать функцию  методом наискорейшего спуска, заканчивая вычисления при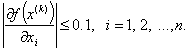

Решение. Найдем частные производные:

1-й шаг. Положим Х(0) = (0, 0), тогда

Для нахождения точки минимума функции Ф0(H) используем метод Пауэлла. Поскольку шаг H изменяется в пределах 0 < H < 1, то за первоначальное значение примем  H = 0,  а H = 0.5. Таким образом, находим H0 = 0.2.

Значит, Х(1) =(0, 0) – 0.2(1, -1) = (-0.2, 0.2).

Вычислим значение производных: F(-0.2, 0.2) = (0.4, 0.4). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

2-й шаг. Составим функцию:

Снова используем метод Пауэлла, полагая H = 0 и H = 0.5, Находим H1 = 0.3.

Значит, Х(2) =(-0.2,0.2) – 0.3(0.4,-0.4) = (-0.32, 0.08).

Вычислим значение производных: F(-0.32, 0.08) = (0.28, -0.2). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

3-й шаг. Составим функцию:

Используем метод Пауэлла, полагая H = 0 и H = 0.5, Находим H2 = 0.2327.

Значит, Х(3) =(-0.32-0,23270,28; 0.08+0.23270.2)=(-0.3852; 0.1265). Вычислим значение производных: F(х(3)) = (0.1031, 0.1442). Условия завершения поиска не выполняются, поэтому переходим к следующему шагу.

4-й шаг. Составим функцию:

Используем метод Пауэлла, полагая H = 0 и H = 0.5, Находим H2 = 0.27.

Значит, Х(4) =(-0.3852-0,270,1031; 0.1265-0.270.1442)=(-0.413; 0.0876). Вычислим значение производных: F(х(4)) = (0.0864, -0.0614). Условия завершения поиска  выполняются,  поэтому требуемая точность достигнута и

< Предыдущая		Следующая >