9.1.2. Пример выполнения задачи 1
Задача. Найти точки локального экстремума функции и значения функции в них:
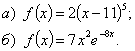
Решение. а) Находим производную: ![]()
Решим уравнение ![]()
![]() Х=11.
Х=11.
Функция F(X) определена и непрерывна на всей числовой оси. Поэтому точка Х=11 является критической точкой. Других критических точек нет, так как ![]() существует всюду.
существует всюду.
Исследуем критическую точку, определяя знак первой производной, слева и справа от неё.
Таблица 33
|
X |
0 |
11 |
20 |
|
|
+ |
0 |
+ |
|
F(X) |
Возрастает |
|
Возрастает |
Так как на всей числовой оси функция возрастает, то она не имеет экстремумов.
Б) Находим производную: ![]()
Решим уравнение ![]()

Функция F(X) определена и непрерывна на всей числовой оси. Поэтому точки Х1=0 и Х2=0,25 являются критическими точками. Других критических точек нет, так как F(X) существует всюду. Исследуем критические точки, определяя знак первой производной, слева и справа от каждой точки.
Таблица 34
|
X |
-1 |
0 |
0.1 |
0.25 |
1 |
|
|
- |
0 |
+ |
0 |
- |
|
F (X) |
Убывает |
|
Возрастает |
|
Убывает |
На интервале (0; 0,25) функция возрастает, а на интервалах (-; 0) и (0,25; +) – убывает.
Значит, Х1=0 – точка минимума, F(0)=0; х2=0,25 – точка максимума, F(0.25)0.0596.
| < Предыдущая | Следующая > |
|---|