8.8. Выбор оптимального маршрута перевозки грузов
Математический аппарат ДП, основанный на методологии пошаговой оптимизации, может быть использован при нахождении кратчайших расстояний, например, на географической карте, представленной в виде сети. Решение задачи по определению кратчайших расстояний между пунктами отправления и пунктами получения продукции по существующей транспортной сети является исходным этапом при решении таких экономических задач, как оптимальное прикрепление потребителей за поставщиками, повышение производительности транспорта за счет сокращения непроизводительного пробега и др.
|
|
Пусть транспортная сеть состоит из 10 узлов, часть из которых соединены магистралями. На рис. 44. показана сеть дорог и стоимости перевозки единицы груза между отдельными пунктами сети, которые проставлены у соответствующих ребер. Необходимо определить маршрут доставки груза из пункта 1 в пункт 10, обеспечивающий наименьшие транспортные расходы.
В задаче имеется ограничение – двигаться по изображенным на схеме маршрутам можно только слева направо, т. е. попав, например, в пункт 7, мы имеем право переместиться только в пункт 10 и не можем возвратиться обратно в 5-й или 6-й. Эта особенность транспортной сети дает право отнести каждый из десяти пунктов к одному из поясов. Будем считать, что пункт принадлежит k-му поясу, если из него можно попасть в конечный пункт ровно за k шагов, т. е. с заездом ровно в (k-1)-й промежуточный пункт. Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, 5 и 6 – ко второму, 2, 3, 4 – к третьему, 1 – к четвертому. Тогда на k-м шаге будем находить оптимальные маршруты перевозки груза из пунктов k-го пояса до конечного пункта. Оптимизацию будем производить с конца процесса, и потому, дойдя до k-го шага, неизвестно, в каком из пунктов k-го пояса окажется груз, перевозимый из первого пункта.
Введем обозначения:
K – номер шага (K = 1, 2, 3, 4);
I – пункт, из которого осуществляются перевозки (I = 1, 2, …, 9);
J – пункт, в который доставляется груз (J = 2, 3, …, 10);
Cij – стоимость перевозки груза из пункта I в пункт J.
Fk(I) – минимальные затраты на перевозку груза на K-м шаге решения задачи из пункта I до конечного пункта.
Очевидно, что минимум затрат на перевозку груза из пунктов K-го пояса до пункта 10 будет зависеть от того, в каком пункте этого пояса мы оказались. Номер I пункта, принадлежащего K-му поясу, будет являться переменной состояния системы на K-м шаге. Поскольку оптимизация осуществляется с конца процесса, то, находясь в некотором пункте I K-го пояса, принимается решение о перемещении груза в один из пунктов (K-1)-го пояса, а направление дальнейшего движения известно из предыдущих шагов. Номер J пункта (K-1)-го пояса будет переменной управления на K–м шаге.
Для первого шага управления (K=1) функция Беллмана представляет собой минимальные затраты на перевозку груза из пунктов 1-го пояса в конечный пункт, т. е. ![]() . Для последующих шагов затраты складываются из двух слагаемых – стоимости перевозки груза Cij из пункта I K-го пояса в пункт J (K-1)-го пояса и минимально возможных затрат на перевозку из пункта J до конечного пункта, т. е. Fk1(J). Таким образом, функциональное уравнение Беллмана будет иметь вид
. Для последующих шагов затраты складываются из двух слагаемых – стоимости перевозки груза Cij из пункта I K-го пояса в пункт J (K-1)-го пояса и минимально возможных затрат на перевозку из пункта J до конечного пункта, т. е. Fk1(J). Таким образом, функциональное уравнение Беллмана будет иметь вид
![]()
Минимум затрат достигается на некотором значении J*, которое является оптимальным направлением движения из пункта 1 в конечный пункт.
На четвертом шаге попадаем на 4-й пояс и состояние системы становится определенным I=1. Функция F4(1) представляет собой минимально возможные затраты по перемещению груза из 1-го пункта в 10-й. Оптимальный маршрут определяется в результате анализа всех шагов в обратном порядке, а выбор некоторого управления J на K-м шаге приводит к тому, что состояние системы на (K-1)-м шаге становится определенным.
Пример 75. Решим сформулированную выше задачу, исходные данные которой приведены на рис. 43.
Решение.1 этап. Условная оптимизация.
1-й шаг. K=1.
F1(I)=Ci10
На первом шаге в пункт 10 груз может быть доставлен из пунктов 7, 8 или 9.
Таблица 29
|
J I |
10 |
F1(i) |
J* |
|
7 |
7 |
7 |
10 |
|
8 |
9 |
9 |
10 |
|
9 |
11 |
11 |
10 |
2-й шаг. K=2.
Функциональное уравнение на втором шаге принимает вид
![]()
Все возможные перемещения груза на втором шаге и результаты расчета приведены в следующей табл. 30:
Таблица 30
|
J I |
7 |
8 |
9 |
F2(i) |
J* |
|
5 |
8+7 |
6+9 |
- |
15 |
7; 8 |
|
6 |
5+7 |
- |
4+11 |
12 |
7 |
3-й шаг. K=3.
![]()
Таблица 31
|
J I |
5 |
6 |
F3(i) |
J* |
|
2 |
4+15 |
- |
19 |
5 |
|
3 |
- |
3+12 |
15 |
6 |
|
4 |
- |
9+12 |
21 |
6 |
4-й шаг. K=4.
![]()
Таблица 32
|
J I |
2 |
3 |
4 |
F3(i) |
J* |
|
1 |
7+19 |
5+15 |
6+21 |
20 |
3 |
2 этап. Безусловная оптимизация.
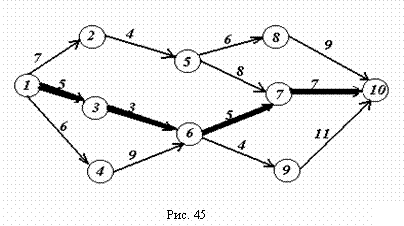
На этапе условной оптимизации получено, что минимальные затраты на перевозку груза из пункта 1 в пункт 10 составляют F4(1)=20. Данный результат достигается при движении груза из 1-го пункта в 3-й. По данным таблицы третьего шага необходимо двигаться в пункт 6, затем – в пункт 7 (см. таблицу второго шага) и из него – в конечный пункт (см. таблицу первого шага). Таким образом, оптимальный маршрут доставки груза: 1 3 6 7 10. На рис. 45 жирными стрелками показан оптимальный путь.
|
|
| < Предыдущая | Следующая > |
|---|