8.5. Двумерная модель распределения ресурсов
Рассмотрим работу схемы на примере. В качестве примера приведем задачу об оптимальном распределении ресурсов между двумя отраслями (между фирмами, хозяйствующими субъектами) на N лет.
Предположим, что планируется деятельность двух отраслей производства на N лет. Начальные ресурсы S0. Средства х, вложенные в первую отрасль в начале года, дают в конце года Прибыль F1(X) и Возвращаются в размере Q1(X)<X; аналогично для второй отрасли: Функция прибыли равна F2(X), а Возврата – Q2(X) (Q2(X)<X).
В конце года все возвращенные средства заново перераспределяются между первой и второй отраслями, новые средства не поступают, прибыль в производство не вкладывается
(последние условия приняты с целью упрощения метода, в случае, если поступают новые средства или часть прибыли вкладывается в производство, задача усложняется, однако, алгоритм метода ДП не изменяется).
Требуется распределить имеющиеся средства S0 между двумя отраслями производства на N лет так, чтобы суммарная прибыль от обеих отраслей за N лет оказалась максимальной.
Пример 72. Приведем решение задачи методом ДП при условии, что S0 = 10000 ед., N = 4, F1(X)= 0.6X, Q1(X) = 0.7X, F2(X) = 0.5X, Q2(X) = 0.8X.
Решение. Процесс распределения средств между двумя отраслями производства разворачивается во времени, решения принимаются в начале каждого года, следовательно, деление на шаги можно сделать следующим образом: номер шага – номер года. Управляемая система – две отрасли производства, а управление состоит в выделении средств каждой отрасли в очередном году.
Параметры состояния к началу K-го года – Sk-1 (K = 1, 2, …, N) – количество средств, подлежащих распределению. Переменных управления на каждом шаге две: Xk – количество средств, выделенных первой отрасли. Но так как все средства Sk-1 распределяются, то Yk = Sk-1-Xk, и поэтому управление на K-м шаге зависит от одной переменной Xk, т. е. Xk(Xk, Sk-1-Xk).
1) Уравнения состояний: Sk = Q1(Xk) + Q2(Sk-1 – Xk) выражают остаток средств, возвращенных в конце K-го года.
2) Показатель эффективности K-го шага – прибыль, полученная в конце K-го года от обеих отраслей: F1(Xk) + F2(Sk-1 – Xk).
1) Суммарный показатель эффективности – целевая функция задачи – прибыль за N лет:
![]()
4) Пусть Zk*(Sk-1) – условная оптимальная прибыль за N-K+1 лет, начиная с K-го года включительно, при условии, что имеющиеся на начало K-го года средства Sk-1 в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за N лет:
Zmax = Z1*(S0).
5) Уравнения Беллмана имеют вид:

Проведем расчет для конкретных данных.
Уравнение состояний примет вид: Sk = 0.7Xk+0.8(Sk-1-Xk) или Sk = 0.8Sk-1-0.1Xk.
Целевая функция K-го шага: 0.6Xk+0.5(Sk-1-Xk)=0.1Xk+0.5Sk-1.
Целевая функция задачи: ![]()
Функциональные уравнения (уравнения Беллмана):
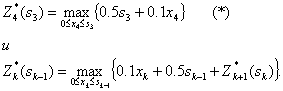
Далее проводим условную оптимизацию.
4-й шаг. Используем уравнение (*). Обозначим через Z4 функцию, стоящую в скобках, Z4 = 0.1X4+0.5S3; функция Z4 – линейная возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала [0, S3] (рис. 42).
|
|
Следовательно, Z4*(S3) = 0.6S3 при X4*(S3) = S3.
3-й шаг. Уравнение
![]()
Находим S3 из уравнений состояний: S3 = 0.8S2-0.1X3 и, подставив его выражение в правую часть уравнения, получаем:

Как и в предыдущем случае, максимум достигается при X3 = S2; т. е. Z3*(S2)=1.02S2 при X3*(S2) = S2.
2-й шаг. Из уравнения состояний: S2 = 0.8S1-0.1X2, поэтому первое функциональное уравнение при K=2 примет вид:
![]()
Линейная относительно X2 Функция Z2* = 1.31S1-0.002X2 убывает на отрезке [0, S1], и поэтому ее максимум достигается при Х2 = 0 (рис. 43).
|
|
При этом: Z2*(S1) = 1.316S1, при X2*(S1) = 0.
1-й шаг. S1 = 0.8S0-0.1X1. Первое функциональное уравнение при K=1 имеет вид:
![]()
Как и в предыдущем случае, максимум достигается в начале отрезка, т. е.: Z1*(S0)=1.5528S0 при X1*(S1)=0.
На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получаем:
Zmax = Z1*(10000), Zmax = 15528.
Далее:
X1* = 0, Y1* = s0 = 10000
(все средства выделяются второй отрасли)
S1* = 0.810000-0.10 = 8000 X2* = 0, Y2* = S1 = 8000
(все средства выделяются второй отрасли)
S2* = 0.88000-0.10 = 6400 X3* = 6400, Y3* = 0
(все средства выделяются первой отрасли)
S3* = 0.86400-0.16400 = 4480 X4* = 4480, Y4* = 0
(все средства выделяются первой отрасли).
Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 10000 ед., равна 15528 ед. при условии, что первая отрасль получает по годам (0; 0; 6400; 4480), а вторая отрасль соответственно (10000; 8000; 0; 0).
| < Предыдущая | Следующая > |
|---|

