7.6. Теоремы Куна - Таккера

  До этого были построены условия Куна – Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна – Таккера тесно связаны с необходимыми условиями оптимальности. В данном разделе рассматриваются строгие формулировки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования.

Теорема 1. Необходимость условий Куна – Таккера.

Рассмотрим задачу нелинейного программирования (18) – (20). Пусть F, G, H – дифференцируемые функции, а х* - допустимое решение данной задачи. Положим  I={J| Gj(X*)=0}. Далее пусть  при При K=1, . . . , K линейно независимы. Если х* - оптимальное решение задачи нелинейного программирования, то существует такая пара векторов (U*, V*), что (X*, U*, V*) является решением задачи Куна – Таккера (21) – (25).

Условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами:

  все ограничения в виде равенств и неравенств содержат линейные функции;

  все ограничения в виде неравенств содержат вогнутые функции, все ограничения-равенства – линейные функции, а также сществует по крайней мере одна допустимая точка х, которая расположена во внутренней части области, определяемой ограничениями-неравенствами. Другими словами, существует такая точка , что

Если условие линейной независимости в точке оптимума не выполняется, то задача Куна – Таккера может не иметь решения.

Пример 69. Минимизировать

При ограничениях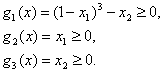

Решение. На рис. 40  изображена область допустимых решений сформулированной выше нелинейной задачи. Ясно, что оптимальное решение этой задачи есть Покажем, что условие линейной независимости не выполняется в точке оптимума.

Так как  то I = {1, 3}. Далее

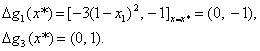
Видно, что векторы  и  линейно зависимы, т. е. условие линейной независимости в точке Х* = (1, 0) не выполняется.

Запишем условия Куна – Таккера и проверим, выполняются ли они в точке (1, 0). Условия (21), (24) и (25) принимают следующий вид:

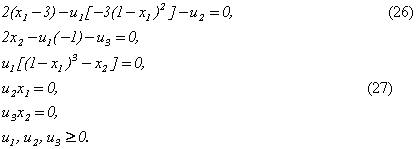
При Х* = (1, 0) из уравнения (26) следует, что U2 = -4, тогда как уравнение (27) дает U2 = 0. Следовательно, точка оптимума не является точкой Куна – Таккера.

Замечание. Нарушение условия линейной независимости не обязательно означает, что точка Куна – Таккера не существует.

Теорему Куна – Таккера можно использовать для доказательства того, что заданная допустимая точка, удовлетворяющая условию линейной независимости, не является оптимальной, если она не удовлетворяет условиям Куна – Таккера. С другой стороны, если в этой точке условия Куна – Таккера выполняются, то нет гарантии, что найдено оптимальное решение нелинейной задачи. В качестве примера рассмотрим следующую задачу нелинейного программирования.

Пример 70. Минимизировать F(X) = 1 – X2

При ограничении

Решение. Здесь

Запишем условия Куна – Таккера:

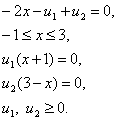
Так как ограничения содержат линейные функции, условие линейной независимости выполняется во всех допустимых точках. Видно, что Х = 3 – точка оптимума. Рассмотрим допустимое решение Х = 2. Для того, чтобы доказать его неоптимальность, проверим выполнение полученных условий Куна – Таккера. Из уравнений (28), (29) следует, что  U1 = U2 = 0; однако значения Х = 2,  U1 = U2 = 0 не удовлетворяют исходному уравнению. Следовательно, по Теореме 1, точка  Х = 2 не может быть оптимальной.

С другой стороны, решение Х = U1 = U2 = 0 удовлетворяет системе всех полученных первоначально неравенств и уравнений и, следовательно, определяет точку Куна – Таккера, однако оптимальным не является. Согласно Теореме 1, условия Куна – Таккера должны выполняться в точке оптимума Х = 3. Нетрудно проверить, что решение Х = 3, U1 = 0, U2 = 6 удовлетворяет условиям Куна – Таккера.

Следующая теорема устанавливает условия, при выполнении которых точка Куна – Таккера автоматически соответствует оптимальному решению задачи нелинейного программирования.

Теорема 2. Достаточность условий Куна – Таккера

Рассмотрим задачу нелинейного программирования

Минимизировать F(X)

При ограничениях

Пусть целевая функция F(X) выпуклая, все ограничения в виде неравенств содержат вогнутые функции Gj(X), J=1, … , J, а ограничения в виде равенств содержат линейные функции Hk(X), удовлетворяющие условиям Куна – Таккера

То х* - оптимальное решение задачи нелинейного программирования.

Замечание. Если условия теоремы 2 выполняются, то нахождение точки Куна – Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему можно использовать для доказательства оптимальности данного решения.

Пример 71. Минимизировать

При ограничениях

Решение. С помощью теоремы 2 докажем, что решение  является оптимальным. Имеем

Так как матрица Hf(X) положительно полуопределена при всех Х, функция F(X) оказывается выпуклой. Первое ограничение в виде неравенства содержит линейную функцию G1(X), которая одновременно является как выпуклой, так и вогнутой. Для того, чтобы показать, что функция G2(X) является вогнутой, вычислим

Поскольку матрица  отрицательно определена, функция G2(X) является вогнутой. Функция H1(X) входит в линейное ограничение в виде равенства. Следовательно, все условия Теоремы 2 выполнены; если мы покажем, что Х* = (1, 5) – точка Куна – Таккера, то действительно установим оптимальность решения Х*.

Условия Куна – Таккера для данного примера имеют вид

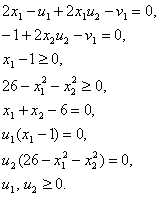
Точка Х* = (1, 5) удовлетворяет полученным ограничениям и, следовательно, является допустимой. Полученные уравнения принимают следующий вид:

Положив V1 = 0, получим U2 = 0.1 и U1 = 2.2. Таким образом, решение Х* = (1, 5),  U* = (2.2, 0.1) и V1 = 0 удовлетворяет условиям Куна – Таккера. Поскольку условия Теоремы 2 выполнены, то Х* = (1, 5) – оптимальное решение задачи. Заметим, что существуют также и другие значения U1, U2, V1, которые удовлетворяют условиям Куна – Таккера, построенным для задачи.

Замечание.

1) Для встречающихся на практике задач условие линейной независимости, как правило, выполняется. Если в задаче все функции дифференцируемы, то точку Куна – Таккера следует рассматривать как возможную точку оптимума. Таким образом, многие из методов нелинейного программирования сходятся к точке Куна – Таккера.

2) Если условия теоремы 2 выполнены, точка Куна – Таккера в то же время оказывается точкой глобального минимума. К сожалению, проверка достаточных условий весьма затруднительна, и, кроме того, прикладные задачи часто не обладают требуемыми свойствами. Следует отметить, что наличие хотя бы одного нелинейного ограничения в виде равенства приводит к нарушению предположений теоремы 2.

3) Достаточные условия, установленные теоремой 2, можно обобщить на случай задач с невыпуклыми функциями, входящими в ограничения в виде неравенств, невыпуклыми целевыми функциями и нелинейными ограничениями-равенствами.

< Предыдущая		Следующая >