7.3. Экономическая интерпретация множителей Лагранжа

Множители Лагранжа рассматривались выше как параметры, значения которых выбираются таким образом, чтобы выполнялись ограничения задачи. С экономической точки зрения множители Лагранжа интерпретируются как неявные (теневые) цены ресурсов, определяемых ограничениями; оптимальные значения множителей Лагранжа играют важную роль в анализе чувствительности решений. Для того, чтобы пояснить эту интерпретационную схему, рассмотрим следующую оптимизационную задачу с двумя переменными и одним ограничением в виде равенства:

Минимизировать

При ограничении

Где постоянная величина B1 характеризует наличие некоторого ресурса.

Предположим, что стационарная точка функции L соответствует глобальному минимуму.

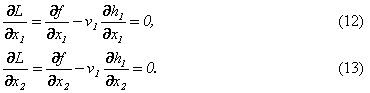
Пусть  - оптимальное значения множителя Лагранжа, а  - оптимальное решение задачи. Далее, пусть минимум функции L(X; V1) при  достигается в точке , причем  и . Очевидно, что оптимальные значения  связаны функциональной зависимостью с величиной B1, задающей границу наличия дефицитного ресурса.

Изменения F0 (оптимального значения F), обусловлены изменениями B1, описываются частной производной . По правилу дифференцирования сложной функции имеем

.   (14)

Дифференцируя обе части ограничений , получаем

.  (15)

Умножим обе части равенства (15)  на  и вычтем из (14):

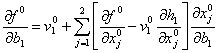.  (16)

Так как Х0 и  удовлетворяют уравнениям (12) и (13), равенство (16) приводится  к виду

.  (17)

Таким образом, из формулы (17) следует, что скорость изменения оптимального значения F, вызываемого изменением B1, определяется оптимальным значением множителя Лагранжа . Другими словами, величина изменения оптимального значения целевой функции,

Обусловленного единичным увеличением правой части ограничения. В зависимости от знака  значения F0 при изменении B1 могут увеличиваться или уменьшаться.

< Предыдущая		Следующая >