5.5. Свойства функций нескольких переменных
В основном мы остановимся на свойствах функций, которые имеют широкое применение в экономических исследованиях, в экономической практике анализа и принятия решений.
Путь имеется функция нескольких переменных Y=F(X1, …, хN), где XiXi, YY и область определения будем рассматривать как наборы-векторов (X1, …, хN), на которых функция определена.
Мы уже рассматривали для функции одной переменной определение монотонной функции.
Для функций двух переменных также определяются понятия возрастания или убывания (монотонности) функции.
Определение. Функция Z = f(х, у) называется Возрастающей ( убывающей ) по переменной 
на интервале (
), если для х1 < х2 из интервала () верно:
.
Другими словами, рассматривается условие возрастания (убывания) функции одной переменной Z = f(х, у) при фиксированном значении У.
Аналогичным образом определяется возрастание (убывание) функции по второй переменной У: функция F(х, у) возрастает (убывает) по переменной У на интервале (
), если для Y1 < Y2 из интервала () верно:
,
Т. е. определяется возрастание (убывание) функции по У при фиксированном Х.
Графически сказанное означает следующее. Допустим, построен график функции Z = f(х, у), который, как известно, представляет собой поверхность в трехмерном пространстве. Рассмотрим графическую иллюстрацию возрастающей функции по Х. Уравнение У=
является частным случаем линейной функции. Графиком функции У= Является плоскость, которая проходит через прямую У= плоскости ХОУ перпендикулярно ей, т. е. параллельно оси 0Z.
Результатом сечения поверхности графика плоскостью У= является кривая, которая соответствует графику функции F(х, ), рассматриваемой как функция одной переменной Х При фиксированном . Тогда понятие монотонности по Х функции F(х, у) можно рассматривать как условие возрастания или убывания функции одной переменной.
Аналогичным образом интерпретируется условие монотонности по переменной У при фиксированном Х.
Иллюстрация сказанного приведена на рис. 29.
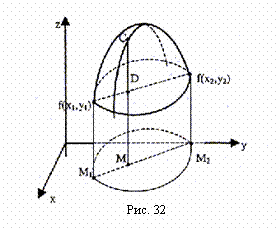
Рис. 30 иллюстрирует ситуацию, в которой функция Z=F(X, Y) убывает по переменной У при фиксированном 
.
|
|
Функция, изображенная на рис. 31 убывает по обеим переменным.
Мы проанализировали изменение функции в сторону возрастания или убывания по одной из переменных, считая вторую фиксированной. Иногда возникает необходимость изучить изменение функции в случае, когда меняются обе переменные.
Следовательно, прежде всего на наборах-векторах из исследуемого множества М должно быть определено отношение порядка. Это так, если, например, аргументы функции имеют числовую природу или есть элементы линейного пространства. И тогда определение возрастающей или неубывающей функции многих переменных можно было бы дать в точности так же, как и для функции одной переменной.
Определение. Функция у(Х) называется Возрастающей (убывающей) на множестве М, если из того, что Х1, Х2 М и Х1 < Х2 вытекает, что у1 < у2 (у1 > у2); функция у(Х) называется Неубывающей (невозрастАющей) на множестве М, если из того, что Х1, Х2М и Х1 Х2 вытекает, что у1 у2 (у1 у2).
Но неравенство Х1 < Х2 Для векторов понимается как строгое неравенство для всех компонент, что является весьма ограничительным. По этой и другим причинам из двух определений комбинируют только одно: функция У(Х) Называется Возрастающей (убывающей) На множестве М, если из того, что Х1, Х2 М И Х1 Х2 Вытекает, что У1 У2 (у1 У2).
При необходимости уточняют характер возрастания или убывания функции многих переменных.
Пример 41. Возрастающими являются рассмотренные выше функции:
1) объем прямоугольного параллелепипеда V = аBС, Где А, B, с — Его длина, ширина и высота;
2) площадь треугольника, вычисляемая по формуле Герона 
Где А, B, с — длины трех его сторон, а Р= (а + B + С)/2 — Полупериметр.
Определение. Функция F, область определения которой симметрична отноСительно нуля, называется Четной (нечетной), если F(—X) = F(X) (F(-X) = —F(X)) для любого ХD(F).
Пример 42. Функция «длина вектора» является четной.
Определение. Функция F называется Ограниченной сверху (снизу) на множестве М, если существует т такое, что f(X) т (F(X)M) для любого Х М. Функция, ограниченная и снизу, и сверху, называется ОграниЧенной на этом Множестве.
Определение. Функция F называется Выпуклой на выпуклом множестве М, если для любых двух точек М(х1, у1) и М(х2, у2) этого множества и любого числа 0 1 верно, что
.
Определение. Функция F называется Вогнутой (выпуклой вверх) На множестве М, если для любых двух точек М(х1, у1) и М(х2, у2) этого множества и любого числа 0 1 верно, что
.
На рис. 32 приведена геометрическая иллюстрация вогнутости функции двух переменных. Для функции двух переменных вогнутость геометрически означает, что любая плоскость, проведенная через точки (X1, Y1, F(X1, Y1)), (X2, Y2, F(X2, Y2)), лежит под графиком функции. В нашем случае:
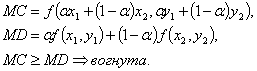
Применяя критерий Сильвестра к матрице вторых производных, можно сформулировать условие выпуклости функции.
Утверждение. Если все угловые миноры 
Положительны при ХU D(F), то функция F(X) выпукла на этом множестве U.
Пример 43. Выяснить, является ли функция 
выпуклой.
Решение. Запишем матрицу вторых производных (матрицу Гессе):
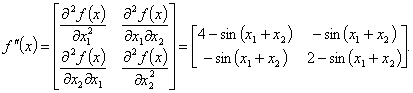
Найдем угловые миноры этой матрицы
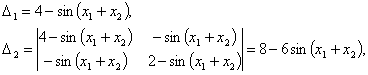
Убеждаемся, что 
при всех Х D(F), т. е. функция F(X) Выпукла.
Пример 44. Убедиться в выпуклости функции 
Решение. Запишем матрицу вторых производных
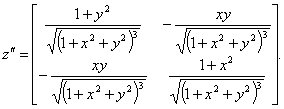
Найдем угловые миноры этой матрицы
Легко убедиться, что при всех Х, Y D(F), т. е. функция Z=F(X, Y) Выпукла.
Из функции многих переменных можно получить «много» функций одной переменной.
Пусть У = Y=Y(X1, …, хN) — Функция П Переменных. Фиксируем значения переменных 
, а Х1 Пусть изменяется. Тогда получим функцию одной переменной: У1 = у(х1, )=у1(х1). Теперь ясно, как понимать выражение «функция Y(X1, …, хN) Возрастает по Х1 При х2 =
» — это говорится про функцию У1(х1). Аналогичным образом нужно понимать и подобные утверждения о четности или нечетности функции по х1 при Х2= и т. п.
Пример 45. Рассмотрим некоторые примеры функций:
функция Z=X – Y возрастает по Х при любом У и убывает по У при любом Х;
функция Z=X2Y является четной по Х при любом У и нечетной по У при любом Х;
функция Z=(2+у)Sinx – периодическая по Х при любом У.
| < Предыдущая | Следующая > |
|---|
