4. Одномерная оптимизация. Методы исключения интервалов

  До этого рассматривался вопрос анализа «в статике», который заключается в том, чтобы определить, является ли данное решение оптимальным. Для этого были построены необходимые и достаточные условия оптимальности решения. Далее мы переходим к изучению вопроса  анализа «в динамике», связанного с нахождением оптимального решения. С этой целью ниже рассматривается ряд одномерных методов поиска, ориентированных на нахождение точки оптимума внутри заданного интервала. Методы поиска, которые позволяют определить оптимум функции одной переменной путем последовательного исключения подынтервалов и, следовательно, путем уменьшения интервала поиска, носят название Методов исключения интервалов.

Ранее было дано определение Унимодальной функции. Унимодальность функций является исключительно важным свойством. Фактически все одномерные методы поиска, используемые на практике, основаны на предположении, что исследуемая функция в допустимой области, по крайней мере, обладает свойством унимодальности. Полезность этого свойства определяется тем фактом, что для унимодальной функции F(X) сравнение значений F(X) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точка оптимума отсутствует.

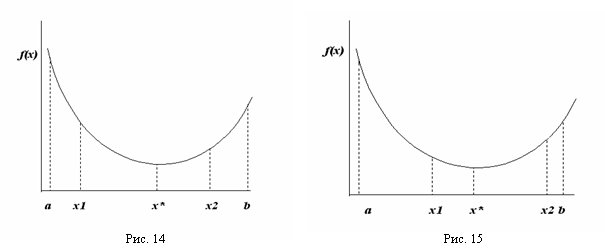
Теорема. Пусть функция F унимодальна на замкнутом интервале , а её минимум достигается в точке х*. Рассмотрим точки х1 и х2, расположенные в интервале таким образом, что A < X1 < X2 < B. Сравнивая значения функции в точках х1 и х2, можно сделать следующие выводы:

1)  Если F(X1) > F(X2), то точка минимума F(X) не лежит в интервале (а, х1), т. е.  (см. рис. 14).

2)  Если F(X1) < F(X2), то точка минимума не лежит в интервале (х2, B), т. е.  (см. рис. 15).

Замечание. Если F(X1) = F(X2), то можно исключить оба крайних интервала  (а, х1) и (х2, B); при этом точка минимума должна находится в интервале (х1, х2).

Согласно приведенной выше теореме, которую иногда называют Правилом исключения интервалов, можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило исключения интервалов, устраняет необходимость полного перебора всех допустимых точек. Несомненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значений функции F(X) в заданных точках X с помощью прямых расчетов или имитационных экспериментов.

Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:

 Этап установления границ интервала, на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума;

 Этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины.

В данном разделе рассматриваются методы решения одномерных задач оптимизации вида

Где Х – скаляр, A и B – соответственно концы интервала, из которого берутся значения переменной Х.

В основном рассматриваются алгоритмы, связанные с построением улучшающей последовательности. Решением задачи называется Х*, при котором F(X*)  F(X) для любого значения . При практическом решении задач не будем различать два значения Xi и Xi+1, если |Xi-Xi+1|, где  - задаваемая погрешность решения.

< Предыдущая		Следующая >