4.3. Метод золотого сечения

 Метод золотого сечения также является последовательным методом минимизации. Опираясь на свойства золотого сечения отрезка, этот метод использует найденные значения F(X) более рационально, чем метод деления отрезка пополам, что позволяет переходить к  очередному отрезку, содержащему точку Х* после вычисления одного, а не двух значений F(X).

Метод основан на делении текущего отрезка [A; B], где содер­жится искомый экстремум, на две неравные части, подчиняющие­ся правилу золотого сечения, для определения следующего отрез­ка, содержащего максимум.

Правило золотого сечения: Отношение всего Отрезка к большей его части равно отношению большей части от­Резка к меньшей. Ему удовлетворяют две точки с и D, располо­Женные симметрично относительно середины отрезка:

Путем сравнения  F(с) И F(D) Определяют следующий отрезок, где содержится максимум. Если F(D) > F(с), то в качестве сле­дующего отрезка выбирается отрезок [с, B], в противном слу­чае — отрезок [а, D].

Новый отрезок снова делится на неравные части по правилу золотого сечения. Следует отметить, что точка D является и точ­кой золотого сечения отрезка [с, B], Т. е.

Поэтому на каждой следующей итерации (кроме "запуска" метода на исходном отрезке) нужно вычислять только одно зна­чение критерия оптимальности.

Существуют аналитические формулы для расчета новой точ­ки на отрезке, где находится максимальное значение F(X).

Золотое сечение отрезка [A; B] осуществляется двумя точками:

  (3)

Причем Х1 есть вторая точка золотого сечения отрезка [A; X2], а Х2 – первая точка золотого сечения отрезка [X1; B].

Зная одну из точек золотого сечения отрезка [A; B], другую можно найти по одной из формул

X1 = A + B - X2, X2 = A + B – X1. (4)

Пусть F(X)  Q[A; B] и требуется найти точку минимума Х* функции F(X) на [A; B]. Построим последовательности {An}, {Bn}, {}, N = 1, 2, …, следующим образом:

  (5)

Первая и вторая точки золотого сечения (3) отрезка [An-1; Bn-1].

Для определения чисел An, Bn, По найденным An-1, Bn-1, Необходимо выполнить следующие операции:

1)  найти одну из точек золотого сечения отрезка [An-1; Bn-1] по известной другой точке , используя формулы (4) или (3);

2)  вычислить значение F(X) во вновь найденной точке золотого сечения;

3) сравнить значения  и  и найти An, bn, Xn по формулам (5).

Таким образом, на каждом шаге определения An, Bn и , N=2, 3, …, требуется вычисление одного значения F(X). Положив , найдем точку минимума Х* с точностью N:

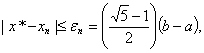  (6)

Откуда следует, что число шагов N метода золотого сечения, обеспечивающее заданную точность  нахождения точки Х*, должно удовлетворять неравенству:

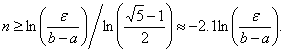  (7)

Либо можно принять другое условие окончания поис­ка — величина отрезка, содер­жащего максимум, меньше за­данной погрешности.

Метод золотого сечения обеспечивает более быструю сходимость к реше­нию, чем многие другие ме­тоды, и применим, очевидно, только для одноэкстремальных функций, т. е. функций, содержащих один экстремум того типа, который ищется в задаче.

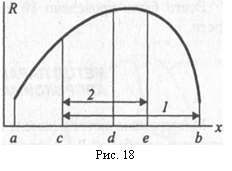
На рис. 18 приведены два этапа поиска максимума функ­ции методом золотого сече­ния: 1 – интервал,  включающий в себя искомый максимум функции после первого этапа (первого золотого сечения в точках C и D); 2 – то же, после второго этапа (новая точка E и старая точка D).

 Пример 17. Найти минимальное значение F* и точку минимума Х* функции На отрезке [1.5; 2]. Точку Х* Найти с точностью =0,05.

Решение. Вычисления проведем по формулам (5) представив результаты в табл. 12.

Таблица 12

N	n	An	Bn	X1(n)	X2(n)	F(x1(n))	F(x2(n))	Примечание
1	0,309	1,500	2,000	1,691	1,809	-92,049	-91,814
2	0,191	1,500	1,809	1,618	1,691	-91,464	-92,049
3	0,118	1,618	1,809	1,691	1,736	-92,049	-92,138
4	0,073	1,691	1,809	1,736	1,764	-92,138	-92,084
5	0,045				1,736		-92,138

 Первоначальные значения Х1 И х2 находим по формулам (3), а значения точности   по формуле (6).

Из таблицы получаем  

Заметим, что если воспользоваться формулой (7), то необходимое число шагов N можно определить заранее. В нашем случае N  4,79, т. е. N = 5, и отпадает необходимость во втором столбце табл. 12.

Пример 18. Найти точку минимума Х*И минимум F* функции F(X)=X2+3X(Lnx-1) на отрезке [0.5; 1] С точностью =0,05.

Решение. Вычисления представим в табл. 13.

Таблица 13

N	n	An	Bn	Х1(n)	X2(n)	F(x1(n))	F(x2(n))	Примечание
1	0,309	0,5	1	0,691	0,809	-2,362	-2,287
2	0,191	0,5	0,809	0,618	0,691	-2,364	-2,362
3	0,118	0,5	0,691	0,573	0,618	-2,348	-2,364
4	0,073	0,573	0,691	0,618	0,646	-2,364	-2,368
5	0,045			0,646		-2,368

 Следовательно, Х* 0,646, и  F* F (0,646) = -2,368.

< Предыдущая		Следующая >