02. Геометрическая интерпретация

G=x2-x1 (4)

При ограничениях

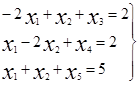. (5)

Удобнее решить задачу максимизации q/ = - q= x1-x2. (6)

Имеется m=3 базисных переменных и n-m=2 свободных. Выразим базисные переменные через свободные .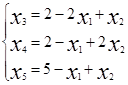

Область допустимых значений: xi≥0, . Построим прямые x3, x4, x5 на плоскости x1, x2:

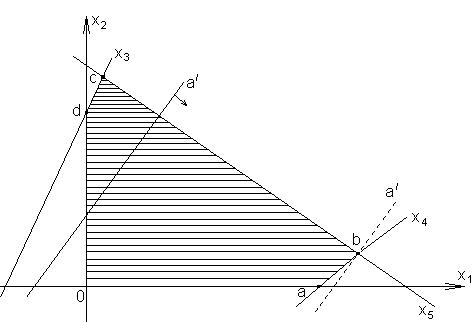
Для каждой прямой xi переменных xi=0. В точках пересечения 2-х прямых в нуль обращаются две переменные, что соответствует базисному решению. Вершины многоугольника допустимых решений соответствуют допустимым базисным решениям. Выражение (6) определяет прямую, причём увеличение q/ соответствует перемещению прямой в направлении стрелки. Эта прямая должна проходить через область допустимых решений. Максимум q/ получим в крайнем положении прямой (пунктир). Таким образом, решение, обращающее в максимум целевую функцию q/, обязательно лежит среди допустимых базисных решений. Т. к. их число, конечно, то можно найти все допустимые базисные решения и для каждого из них вычислить значение q/. Окончательным решением будет, то для которого q/ будет максимально.

Наиболее распространённый метод такого перебора решений – это симплекс – метод.

Алгебра симплекс – метода.

Существо метода состоит в следующем. Находим какое-нибудь базисное решение. Далее проверяем, не достигнут ли уже максимум целевой функции. Если нет, то ищем новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение q/. Затем процедуру повторяем. Для перехода к новому допустимому базисному решению одну из свободных переменных следует сделать базисной. При этом она станет отличной от нуля и будет возрастающей. Если какая либо свободная переменная входит в целевую функцию со знаком «+», т. е. при её увеличении целевая функция увеличивается, то максимум не достигнут и данную переменную следует сделать базисной (отличной от нуля).

Математическое описание.

Использование графического способа удобно только при решении задач ЛП с двумя переменными. При большем числе переменных необходимо применение алгебраического аппарата. В данной главе рассматривается общий метод решения задач ЛП, называемый симплекс-методом.

Информация, которую можно получить с помощью симплекс-метода, не ограничивается лишь оптимальными значениями переменных.

Процесс решения задачи линейного программирования носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры, реализуемые в рамках симплекс-метода, требуют применения вычислительных машин - мощного средства решения задач линейного программирования.

Симлекс-метод - это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач.

Правая и левая части ограничений линейной модели могут быть связаны знаками <=, = и =>. Кроме того, переменные, фигурирующие в задачах ЛП, могут быть неотрицательными или не иметь ограничения в знаке. Для построения общего метода решения задач ЛП соответствующие модели должны быть представлены в некоторой форме, которую назовем стандартной формой линейных оптимизационных моделей. При стандартной форме линейной модели.

1. Все ограничения записываются в виде равенств с неотрицательной правой частью;

2. Значения всех переменных модели неотрицательны;

3. Целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1. Исходное ограничение, записанное в виде неравенства типа <= ( =>), можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).

Например, в левую часть исходного ограничения

5X1 + 100X2 <= 1000

Вводится остаточная переменная S1 > 0 , в результате чего исходное неравенство обращается в равенство

5X1 + 100X2 + S1 = 1000 , S1 => 0

Если исходное ограничение определяет расход некоторого ресурса, переменную S1 следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.

Рассмотрим исходное ограничение другого типа:

X1 - 2X2 => 0

Так как левая часть этого ограничения не может быть меньше правой, для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную S2 > 0 . В результате получим

X1 - 2X2 - S2 = 0, S2 => 0

2. Правую часть равенства всегда можно сделать неотрицательной, умножая оби части на-1 .

Например, равенство X1 - 2X2 - S2 = 0 эквивалентно равенству - X1 + 2X2 + S2 = 0

3. Знак неравенства изменяется на противоположный при умножении обеих частей на -1.

Например, можно вместо 2 < 4 записать - 2 > - 4 , неравенство X1 - 2X2 <= 0 заменить на - X1 + 2X2 => 0

Переменные

Любую переменную Yi, не имеющую ограничение в знаке, можно представить как разность двух неотрицательных переменных:

Yi=Yi’-Yi’’, где Yi’,Yi’’=>0.

Такую подстановку следует использовать во всех ограничениях, которые содержат исходную переменную Yi, а также в выражении для целевой функции.

Обычно находят решение задачи ЛП, в котором фигурируют переменные Yi’ и Yi’’ , а затем с помощью обратной подстановки определяют величину Yi . Важная особенность переменных Yi’ и Yi’’ состоит в том, что при любом допустимом решении только одна из этих переменных может принимать положительное значение, т. е. если Yi’>0 , то Yi’’=0, и наоборот. Это позволяет рассматривать Yi’ как остаточную переменную, а Yi’’ - как избыточную переменную, причем лишь одна из этих переменных может принимать положительное значение. Указанная закономерность широко используется в целевом программировании и фактически является предпосылкой для использования соответствующих преобразований.

Целевая функция

Целевая функция линейной оптимизационной модели, представлена в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию.

Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например максимизация функции

Z = X1 + 25X2

Эквивалентна минимизации функции

(-Z) = - X1 - 25X2

Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения X1 , X2 , в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.

< Предыдущая		Следующая >