01. Линейное программирование. Постановка задачи

Термин и линейное программирование связывается со следующей задачей. Дана система линейно независимых уравнений с неизвестными х1,….,х2 – система ограничений задач и линейного программирования:

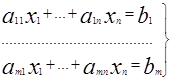, (1)

Где bi≥0. Требуется найти неотрицательное значение переменных (хi≥0), которые удовлетворяют управлениям (1) и обращают в минимум целевую функцию q = c1x1+…+cnxn (2), называемой линейной формой.

Матричная запись:

(3)

Если m<n, то система (1) имеет бесчисленное множество решений. Любое решение системы (1), где xi≥0 будем называть допустимым решением. Среди допустимых решений нужно выбрать такое, которое обращает в минимум целевую функцию.

В ограничения (1) могут входить не равенства aj1x1+..+ajnxn≤bj или aj1x1+..+ajnxn≥bj введя дополнительную переменную xn+j так, чтобы имело место: aj1x1+..+ajnxn+xn+j=bj или aj1x1+..+ajnxn-xn+j=bj что не меняет существа задачи. Задача максимизации сводится к рассмотренной путем замены знака целевой функции .

Базисом называют набор m переменных таких, что определить, составленный из коэффициентов, при этих переменных не равен нулю. Эти переменных называют базисными. Если положить все свободные переменные равными нулю и решить полученную систему m уравнений с m неизвестными, то получим базисное решение. Допустимыми базисными решениями являются такие, которые дают неотрицательные значения базисных переменных.

Следующая >