5. Моделирование поведения потребителя

При изучении поведения потребителя используются функции полезности и спроса. Функции полезности отражают конечные результаты использования различных потребительских товаров и благ.

В пространстве товаров каждой функции полезности соответствует некоторое семейство непересекающихся поверхностей безразличия, соответствующих определенным уровням потребления набора товаров.

Функции полезности могут быть преобразованы в функции покупательского спроса. Для этого необходимо решить задачу оптимального выбора потребителя, т. е. определить какой товар и в каком количестве лучше взять потребителю, что бы максимизировать потребление в рамках своего дохода с учетом цены каждого товара. Математически задача потребительского выбора представляет собой задачу условной оптимизации и формулируется следующим образом:

U(X1,X2...Xn)→max

При ограничении

P1X1+p2X2+...+pnXn=I, где

U(X1,X2...Xn) – функция полезности, j=1,2, … N – число товаров; pj – цена товара; Xj – количество потребляемого товара; I – доход потребителя

Решение задачи условной оптимизации для функции полезности 2-х переменных сводится к решению следующей системы уравнений: 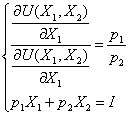, в результате решения которой определяются функции потребительского спроса на товары Х1 и Х2.

При анализе функций спроса важное значение имеет определение таких экономических показателей как коэффициент эластичности спроса относительно дохода потребителя и коэффициент эластичности спроса относительно цены товара.

Эластичность по доходу представляет собой процентное значение увеличения (уменьшения) спроса на товар при увеличении (уменьшении) дохода на один процент.

Товар называют товаром с неэластичным спросом по доходу, если эта эластичность меньше +1, и с эластичным спросом по доходу, если она больше +1.

Эластичность спроса по цене является мерой чувствительности спроса на изменение цены. Различают прямые и перекрестные эластичности по цене. В первом случае измеряется изменение спроса на товар при изменении на 1% его же цены, во втором — при изменении также на 1% цены другого товара. Эластичный спрос по цене наблюдается, если коэффициент эластичности по модулю больше 1, и неэластичный в противном случае. Важное значение при анализе имеет расчет перекрестного коэффициента эластичности, если перекрестный коэффициент эластичности отрицателен, то товары являются дополняющими, если равен нулю — независимыми, если положителен — конкурирующими.

Пример

Решите задачу потребительского выбора, определив функции спроса на товары X1 и X2 при функции полезности потребителя . Рассчитайте спрос на товары Х1 и Х2 согласно следующим исходным данным: доход потребителя составляет I=60 усл. д.е., а цены товаров соответственно равны р1=1, р2=2 усл. д.е.

Решение задачи потребительского выбора сводится к решению следующей системы уравнений:

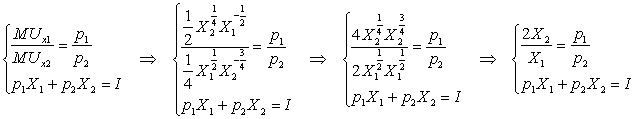Для получения функций спроса необходимо решить полученную систему уравнений в общем виде. Выразим из первого уравнения переменную и подставим во второе уравнение: . Из полученного выражения определим функцию спроса на второй товар: , затем, подставив полученную функцию в выражение для X1, определим функцию спроса на первый товар .

Согласно исходным данным задачи, потребителю при существующих ценах на товар и собственном доходе I=60 усл. ден. ед. необходимо покупать товар Х1 в количестве 40 ед., товар Х2 в количестве 10 ед., при этом функция полезности будет максимальной U=11.25

< Предыдущая