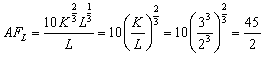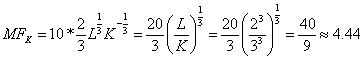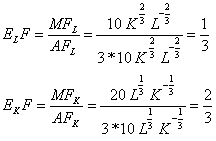4. Использование аппарата производственных функций для анализа экономических систем

Производственной функцией называется аналитическое соотношение, связывающее переменные величины затрат с величиной выпуска продукции.

Производственные функции предназначены для моделирования процесса производства некоторой хозяйственной единицы: отдельной фирмы, отрасли или всей экономики государства в целом. С помощью аппарата производственных функций решаются задачи:

ü оценки отдачи ресурсов в производственном процессе;

ü прогнозирования экономического роста;

ü разработки вариантов плана развития производства;

ü оптимизации функционирования хозяйственной единицы при условии заданного критерия и ограничений по ресурсам.

Общий вид производственной функции:

F = F(R1, R2,...,Ri.,...Rn),

Где F - показатель, характеризующий результаты производства;

Ri - факторный показатель i-го производственного ресурса;

Производственные функции определяются двумя группами предположений: математических и экономических.

Математически предполагается, что производственная функция должна быть непрерывной и дважды дифференцируемой.

Экономические предположения состоят в следующем:

ü при отсутствии хотя бы одного производственного ресурса производство невозможно, т. е. выполняется:

F(0,R2,…,Ri,...,Rn) = ...F(R1,R2,...,0,...Rn) = F(R1, R2,... Ri,..., 0)=0

ü рост использования ресурсов приводит к росту результата производства, т. е. выполняются соотношения:

, при Ri > 0, i = l, 2,...n

ü увеличение затрат одного ресурса приводит к снижению эффективности его использования:

, i = l, 2,...n

Производственные функции позволяют определять средние и предельные показатели, характеризующие производственный процесс: средние отдачи ресурсов; предельные отдачи ресурсов; коэффициенты эластичности выпуска по ресурсам; предельные нормы замещения ресурсов; коэффициенты эластичности замещения ресурсов.

Для двухфакторной производственной функции F(K, L), где K – основные фонды, L - трудовые ресурсы, показатели средней отдачи ресурсов определяются по формулам:

,

Частные производные производственной функции по переменным:

,

Трактуются как предельные ресурсоотдачи. Коэффициент предельной продуктивности показывает на сколько увеличится выпуск продукции с увеличением затрат одного из ресурсов на «малую» величину.

Предельной нормой замещения ресурса К называется характеристика,

Которая показывает, сколько единиц ресурса К может быть высвобождено (привлечено) при увеличении (уменьшении) затрат ресурса L на единицу. Аналогично может быть определена предельная норма замещения ресурса L.

Коэффициенты эластичности выпуска по ресурсам определяются следующими формулами:

,

Эти коэффициенты показывают, на сколько процентов изменится производство при изменении затрат соответствующего производственного ресурса на один процент.

В экономико-математических моделях производства каждая технология графически может быть представлена точкой, координаты которой отражают минимально необходимые затраты ресурсов K и L для производства данного объема выпуска. Множество таких точек образуют линию равного выпуска, или изокванту. Таким образом, производственная функция графически представляется семейством изоквант. Смысл изокванты состоит в том, что одно и то же количество продукции F(K, L)=const может быть произведено при различных сочетаниях ресурсов производства К и L.

Определим основные характеристики производственной функции на примере.

Пример

Производственная функция предприятия имеет вид необходимо определить основные характеристики производства при K=27, L=8. Построить семейство изоквант.

1. Средняя производительность труда:

Стоимость продукции, приходящаяся на единицу трудовых ресурсов

2. Средняя фондоотдача

Стоимость продукции, приходящаяся на единицу основных фондов

3. Предельная производительность труда

Добавочная стоимость продукции, произведенная дополнительной единицей трудовых ресурсов

4. Предельная фондоотдача

Добавочная стоимость продукции, произведенная дополнительной единицей основных фондов

5. Коэффициенты эластичности по каждому из ресурсов

Коэффициент эластичности лежит в интервале от 0 до 1, следовательно, каждая последующая дополнительная единица затрачиваемого ресурса вызывает меньший дополнительный прирост продукции, чем предыдущая.

6. Предельная норма замещения основных фондов на трудовые ресурсы

0,31 единица основных фондов может быть заменена единицей трудовых ресурсов, при этом выпуск продукции останется неизменным.

7. Построение семейства изоквант

Для построения изокванты необходимо производственную функцию приравнять к любой константе и выразить одну переменную через другую. Семейство изоквант представлено на рис. 2.

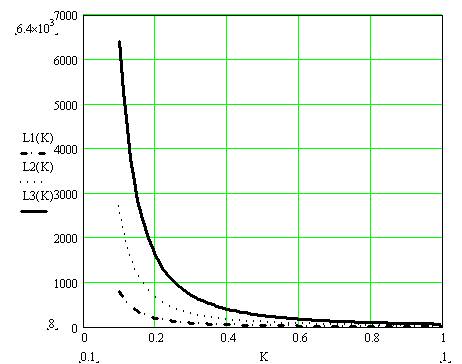
Рис.2. Семейство изоквант

< Предыдущая		Следующая >