13. Метод Ньютона
Основная идея метода Ньютона заключается в итеративном использовании квадратичной аппроксимации целевой функции в текущей точке поиска и минимизации этой аппроксимации. Разложим дважды дифференцируемую целевую функцию ![]() в ряд Тейлора в фиксированной точке
в ряд Тейлора в фиксированной точке ![]() при произвольном приращении аргумента
при произвольном приращении аргумента ![]() , ограничиваясь слагаемыми второго порядка малости,
, ограничиваясь слагаемыми второго порядка малости,
![]() .
.
Пренебрегая слагаемыми выше второго порядка малости и обозначая приращение аргумента ![]() , градиент
, градиент ![]() , матрицу Гессе
, матрицу Гессе ![]() , получим квадратичную функцию
, получим квадратичную функцию
![]() .
.
Вычислим значение аргумента ![]() , которое минимизирует эту функцию. Используя формулы векторного дифференцирования
, которое минимизирует эту функцию. Используя формулы векторного дифференцирования
![]() ,
, ![]() ,
,
Запишем градиент квадратичной функции
![]() .
.
Учитывая необходимое условие минимума ![]() , получим систему линейных алгебраических уравнений (СЛАУ)
, получим систему линейных алгебраических уравнений (СЛАУ)
![]() . (2.1)
. (2.1)
Решая эту систему относительно вектора ![]() , найдем вектор перемещения в точку минимума квадратичной функции
, найдем вектор перемещения в точку минимума квадратичной функции
![]() . (2.2)
. (2.2)
Метод минимизации функции, основанный на формулах (2.1) или (2.2), называется Методом Ньютона. Формулы (2.1) и (2.2) можно представить в виде:
![]() ,
, ![]() .
.
Метод Ньютона минимизирует положительно определенную квадратичную функцию за один шаг из любой начальной точки ![]()
![]() .
.
В случае же минимизации функции общего вида метод Ньютона применяется итерационно. Обозначая в текущей точке поиска ![]() значения градиента
значения градиента ![]() и матрицы Гессе
и матрицы Гессе ![]() , получим на основании равенства (2.1) итерационные формулы метода Ньютона для номеров итераций
, получим на основании равенства (2.1) итерационные формулы метода Ньютона для номеров итераций ![]() из произвольной начальной точки поиска
из произвольной начальной точки поиска ![]() :
:
![]() ,
, ![]() . (2.3)
. (2.3)
Итерации продолжаются до тех пор, пока выполняется условие
![]() ,
,
Где ![]() – допустимая погрешность,
– допустимая погрешность, ![]() . По формулам (2.3) составим алгоритм метода Ньютона.
. По формулам (2.3) составим алгоритм метода Ньютона.
Алгоритм метода Ньютона.
Входные параметры: ![]() – начальная точка поиска,
– начальная точка поиска, ![]() – процедура вычисления функции,
– процедура вычисления функции, ![]() – допустимая погрешность.
– допустимая погрешность.
Выходной параметр ![]() – конечная точка поиска.
– конечная точка поиска.
1. Вычислить ![]() ,
, ![]() .
.
2. Решить СЛАУ ![]() .
.
3. Положить ![]() .
.
4. Если ![]() , то перейти к шагу 1.
, то перейти к шагу 1.
5. Остановиться.
В этом алгоритме на шаге 2 решается система линейных алгебраических уравнений одним из стандартных методов используемой вычислительной системы. Например, в системе MATLAB СЛАУ решается оператором ![]() . Здесь применяется формула (2.1) метода Ньютона. На шаге 2 возможно применение и формулы (2.2), в которой используется обратная матрица Гессе
. Здесь применяется формула (2.1) метода Ньютона. На шаге 2 возможно применение и формулы (2.2), в которой используется обратная матрица Гессе
![]() . (2.4)
. (2.4)
Однако обращение матрицы в формуле (2.4) требует выполнения гораздо большего количества операций, чем решение СЛАУ в (2.3).
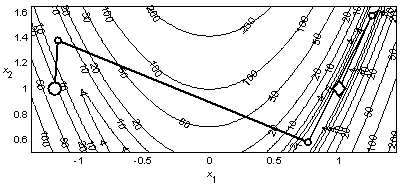
Пример 2.1. На рис. 2.1 представлена траектория поиска минимума квадратичной функции (1.3) методом Ньютона. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 3 итерации и выполнил 19 вычислений функции. Поскольку определение матрицы Гессе в начальной точке поиска и решение СЛАУ (2.1) выполняется с вычислительными погрешностями, то на первой итерации найдено приближение точки минимума с погрешностью 5,3∙10–3. На последующих двух итерациях положение точки минимума уточнено и достигнута конечная погрешность 7,3∙10–23. Сравнивая эти результаты с результатами примеров 1.5 и 1.7, можно убедиться в преимуществе метода Ньютона перед методами циклического покоординатного спуска и наискорейшего спуска при минимизации квадратичной целевой функции.
|
|
|
Рис. 2.1. Минимизация квадратичной функции методом Ньютона |
Пример 2.2. На рис. 2.2 представлена траектория поиска минимума функции Розенброка методом Ньютона. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 9 итераций и выполнил 55 вычислений функции. Сопоставление этих результатов с результатами примеров 1.6 и 1.8 также подтверждает преимущество метода Ньютона по сравнению с методами циклического покоординатного спуска и наискорейшего спуска.
В отличие от формул (1.20) метода наискорейшего спуска, в которых антиградиент ![]() задает только направление поиска, в формулах (2.3) метода Ньютона вектор
задает только направление поиска, в формулах (2.3) метода Ньютона вектор ![]() задает и направление, и шаг перехода в следующую точку поиска.
задает и направление, и шаг перехода в следующую точку поиска.
|
|
|
Рис. 2.2. Минимизация функции Розенброка методом Ньютона |
Умножая равенство (2.2) скалярно на градиент ![]() , получим:
, получим:
![]() .
.
Если матрица Гессе ![]() положительно определенная, то и обратная к ней матрица
положительно определенная, то и обратная к ней матрица ![]() также положительно определенная. В этом случае
также положительно определенная. В этом случае ![]() и вектор
и вектор ![]() определяет направление спуска. Если же матрица
определяет направление спуска. Если же матрица ![]() отрицательно определенная, то вектор
отрицательно определенная, то вектор ![]() определяет направление возрастания функции. В этом случае вектор
определяет направление возрастания функции. В этом случае вектор ![]() приводит в точку максимума квадратичной функции. Условию
приводит в точку максимума квадратичной функции. Условию ![]() отвечает также седловая точка. Поэтому одним из недостатков метода Ньютона является возможное возрастание значений функции
отвечает также седловая точка. Поэтому одним из недостатков метода Ньютона является возможное возрастание значений функции ![]() и расходимость метода для функции общего вида. Другим недостатком является использование матрицы вторых частных производных, требующее дополнительных вычислений.
и расходимость метода для функции общего вида. Другим недостатком является использование матрицы вторых частных производных, требующее дополнительных вычислений.
Метод Ньютона также называют Методом Ньютона – Рафсона. Так как он использует вторые производные целевой функции, это метод второго порядка.
| < Предыдущая | Следующая > |
|---|