03. Экстремум функции многих переменных
Методы безусловной оптимизации предназначены для вычисления экстремума целевой функции многих переменных ![]() , где
, где ![]() – вектор-столбец вещественных переменных, который также можно трактовать как точку
– вектор-столбец вещественных переменных, который также можно трактовать как точку ![]() -мерного пространства
-мерного пространства ![]() . Здесь и далее
. Здесь и далее ![]() – количество переменных, определяющее размерность вектора переменных параметров.
– количество переменных, определяющее размерность вектора переменных параметров.
Точка ![]() называется Точкой локального минимума функции
называется Точкой локального минимума функции ![]() , если существует такое
, если существует такое ![]() , что
, что ![]() для всех
для всех ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() .
.
Точка ![]() называется Точкой строгого локального минимума функции
называется Точкой строгого локального минимума функции ![]() , если существует такое
, если существует такое ![]() , что
, что ![]() для всех
для всех ![]() , удовлетворяющих условиям
, удовлетворяющих условиям ![]() и
и ![]() .
.
Точка ![]() называется Точкой глобального минимума функции
называется Точкой глобального минимума функции ![]() , если
, если ![]() для всех
для всех ![]() .
.
Точка ![]() называется Точкой строгого глобального минимума функции
называется Точкой строгого глобального минимума функции ![]() , если
, если ![]() для всех
для всех ![]() и
и ![]() .
.
Соответствующее значение функции ![]() называется ее Локальным минимумом, Строгим локальным минимумом, Глобальным минимумом, Строгим глобальным минимумом. Глобальный минимум является также и локальным минимумом.
называется ее Локальным минимумом, Строгим локальным минимумом, Глобальным минимумом, Строгим глобальным минимумом. Глобальный минимум является также и локальным минимумом.
Аналогично вводятся понятия Точек максимума и Максимума функции многих переменных. Минимум и максимум имеют общее название Экстремум.
Для определенности методов оптимизации в них полагают, что необходимо найти точку минимума функции. Если для некоторой функции ![]() необходимо найти максимум, то переходят к минимизации функции
необходимо найти максимум, то переходят к минимизации функции ![]() .
.
Задача безусловной минимизации заключается в минимизации функции ![]() при
при ![]() , что представляется в виде:
, что представляется в виде:
![]() ,
, ![]() . (1.1)
. (1.1)
На вектор ![]() не накладывается никаких ограничений (условий), поэтому задача (1.1) минимизации функции
не накладывается никаких ограничений (условий), поэтому задача (1.1) минимизации функции ![]() называется Задачей безусловной оптимизации или Задачей оптимизации без ограничений.
называется Задачей безусловной оптимизации или Задачей оптимизации без ограничений.
Функция, имеющая несколько минимумов или максимумов, называется Многоэкстремальной.
Функция ![]() называется Унимодальной, если она имеет в пространстве параметров
называется Унимодальной, если она имеет в пространстве параметров ![]() единственную точку минимума
единственную точку минимума ![]() .
.
Решение задачи безусловной минимизации (1.1) представляется в виде:
![]() ,
, ![]() .
.
Функция ![]() называется Выпуклой, если
называется Выпуклой, если
![]() (1.2)
(1.2)
Для любых ![]() и любого
и любого ![]() . Функция
. Функция ![]() называется Строго выпуклой, если неравенство (1.2) является строгим для всех различных
называется Строго выпуклой, если неравенство (1.2) является строгим для всех различных ![]() ,
, ![]() и для любого
и для любого ![]() . Функция
. Функция ![]() называется Вогнутой (Строго вогнутой), если
называется Вогнутой (Строго вогнутой), если ![]() выпуклая (строго выпуклая). Выпуклые и вогнутые функции являются непрерывными функциями.
выпуклая (строго выпуклая). Выпуклые и вогнутые функции являются непрерывными функциями.
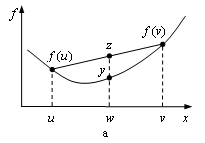
Дадим геометрическую интерпретацию выпуклой функции. Пусть ![]() и
и ![]() – две различные точки и определим точку
– две различные точки и определим точку ![]() с
с ![]() . Заметим, что
. Заметим, что ![]() представляет значение функции в точке
представляет значение функции в точке ![]() , и точка
, и точка ![]() лежит на графике функции (рис. 1.1, а). Величина
лежит на графике функции (рис. 1.1, а). Величина ![]() дает взвешенную сумму
дает взвешенную сумму ![]() и
и ![]() , а точка
, а точка ![]() лежит на графике секущей. Неравенство (1.2) примет вид
лежит на графике секущей. Неравенство (1.2) примет вид ![]() .
.
|
|
|
|
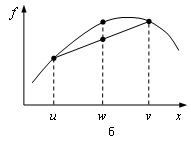
Рис. 1.1. Выпуклая и вогнутая функции |
Таким образом, для выпуклой функции ![]() значение в точках линии сегмента
значение в точках линии сегмента ![]() не больше высоты хорды, соединяющей точки
не больше высоты хорды, соединяющей точки ![]() и
и ![]() (рис. 1.1, а). Для вогнутой функции хорда, соединяющая точки
(рис. 1.1, а). Для вогнутой функции хорда, соединяющая точки ![]() и
и ![]() , проходит не выше графика функции между точками
, проходит не выше графика функции между точками ![]() и
и ![]() (рис. 1.1, б).
(рис. 1.1, б).
Теорема 1.1. Если функция ![]() является выпуклой, то она в любой точке локального минимума достигает своего наименьшего значения.
является выпуклой, то она в любой точке локального минимума достигает своего наименьшего значения.
Доказательство. Пусть ![]() – точка локального минимума функции
– точка локального минимума функции ![]() . Предположим, что в этой точке значение функции
. Предположим, что в этой точке значение функции ![]() не является наименьшим, то есть существует точка
не является наименьшим, то есть существует точка ![]() , для которой
, для которой ![]() . Рассмотрим сечение функции
. Рассмотрим сечение функции ![]() , проходящее через пару точек
, проходящее через пару точек ![]() ,
, ![]() и определяющее функцию одной переменной
и определяющее функцию одной переменной ![]() . Тогда с учетом неравенства (1.2) при
. Тогда с учетом неравенства (1.2) при ![]()
![]() .
.
Отсюда, поскольку ![]() , имеем
, имеем
![]() .
.
Это означает, что в точке ![]() функция
функция ![]() достигает на отрезке
достигает на отрезке ![]() своего наибольшего значения. Для произвольной окрестности точки
своего наибольшего значения. Для произвольной окрестности точки ![]() существует такое малое число
существует такое малое число ![]() , что
, что ![]() принадлежит этой окрестности, то есть
принадлежит этой окрестности, то есть ![]() . Тогда
. Тогда ![]() . А это противоречит тому, что точка
. А это противоречит тому, что точка ![]() есть точка локального минимума. ÿ
есть точка локального минимума. ÿ
Из доказанной теоремы вытекают важные следствия.
Следствие 1.1. Во всех точках локального минимума выпуклая функция ![]() имеет одно и то же значение, равное наименьшему значению
имеет одно и то же значение, равное наименьшему значению ![]() этой функции, а локальный минимум является и глобальным минимумом.
этой функции, а локальный минимум является и глобальным минимумом.
Следствие 1.2. Строго выпуклая функция может иметь не более одной точки локального минимума.
Доказательство. Предположим, что ![]() и
и ![]() – две различные точки локального минимума строго выпуклой функции
– две различные точки локального минимума строго выпуклой функции ![]() и в этих точках функция достигает своего наименьшего значения
и в этих точках функция достигает своего наименьшего значения ![]() . Поскольку функция
. Поскольку функция ![]() строго выпуклая, то неравенство (1.2) является строгим. Тогда для любого
строго выпуклая, то неравенство (1.2) является строгим. Тогда для любого ![]() и
и ![]() имеем:
имеем:
![]() .
.
Мы получили, что ![]() , а это невозможно, так как
, а это невозможно, так как ![]() – наименьшее значение функции. ÿ
– наименьшее значение функции. ÿ
Численные методы решения задачи (1.1) называются Методами безусловной минимизации или Методами минимизации без ограничений. Существуют следующие классы методов безусловной минимизации.
1. Методы нулевого порядка (прямого поиска), не использующие производные целевой функции ![]() .
.
2. Методы первого порядка, использующие первые частные производные целевой функции ![]() .
.
3. Методы второго порядка, использующие матрицу вторых частных производных целевой функции ![]() .
.
Рассматриваемые в данном пособии методы оптимизации предназначены для минимизации унимодальных функций, а также для вычисления локального минимума целевой функции.
Простейшей функцией ![]() нескольких переменных является функция двумерного вектора переменных
нескольких переменных является функция двумерного вектора переменных ![]() ,
, ![]() . Линией уровня функции двух переменных называется линия, во всех точках которой функция принимает постоянное значение. Уравнение линии уровня имеет вид
. Линией уровня функции двух переменных называется линия, во всех точках которой функция принимает постоянное значение. Уравнение линии уровня имеет вид ![]() , где
, где ![]() – некоторая постоянная величина. Изменяя значение
– некоторая постоянная величина. Изменяя значение ![]() , получим семейство линий уровня.
, получим семейство линий уровня.
Для функции трех переменных с ![]() уравнение
уравнение ![]() представляет Поверхность уровня. Для
представляет Поверхность уровня. Для ![]() уравнение
уравнение ![]() представляет Гиперповерхность уровня.
представляет Гиперповерхность уровня.
Пример 1.1. Рассмотрим квадратичную функцию
![]() . (1.3)
. (1.3)
Преобразуем эту функцию, выделяя полный квадрат:
![]() .
.
Это неотрицательная функция и для нее ![]() . Она является суммой квадратов функций
. Она является суммой квадратов функций ![]() и
и ![]() . Приравнивая нулю эти функции, получим систему уравнений:
. Приравнивая нулю эти функции, получим систему уравнений: ![]() ,
, ![]() . Система уравнений имеет единственное решение
. Система уравнений имеет единственное решение ![]() . Это точка строгого глобального минимума функции (1.3) с минимальным ее значением
. Это точка строгого глобального минимума функции (1.3) с минимальным ее значением ![]() , поскольку для всех
, поскольку для всех ![]() будет
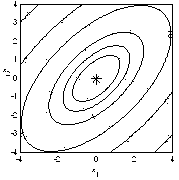
будет ![]() . График функции (1.3) представлен на рис. 1.2, где точка минимума отмечена звездочкой. На рис. 1.3 показаны линии уровня этой функции, которые представляют собой эллипсы с соответствующими значениями функции. Функция (1.3) соответствует эллиптическому параболоиду.
. График функции (1.3) представлен на рис. 1.2, где точка минимума отмечена звездочкой. На рис. 1.3 показаны линии уровня этой функции, которые представляют собой эллипсы с соответствующими значениями функции. Функция (1.3) соответствует эллиптическому параболоиду.
Пример 1.2. Рассмотрим Функцию Розенброка
![]() . (1.4)
. (1.4)
Это также неотрицательная функция. Она представляет собой сумму квадратов функций ![]() и
и ![]() , приравнивая нулю которые имеем систему уравнений:
, приравнивая нулю которые имеем систему уравнений: ![]() ,
, ![]() . Полученная система имеет единственное решение
. Полученная система имеет единственное решение ![]() . Это точка строгого глобального минимума функции Розенброка с минимальным значением функции
. Это точка строгого глобального минимума функции Розенброка с минимальным значением функции ![]() , так как для всех
, так как для всех ![]() будет
будет ![]() .
.
|
|
|
|
Рис. 1.2. График функции |
Рис. 1.3. Линии уровня функции |
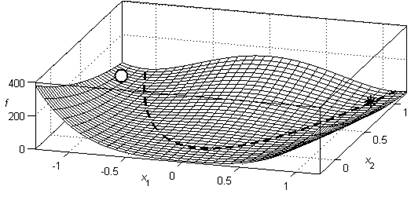
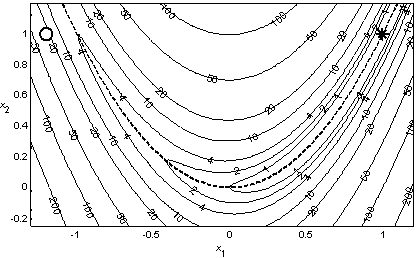
График функции (1.4) представлен на рис. 1.4. На рис. 1.5 показаны линии уровня этой функции, которые вытянуты вдоль параболической линии ![]() , определяющей дно искривленного оврага. Поскольку линии уровня напоминают линии разреза банана, функцию Розенброка называют также «бананообразной» функцией. Она является одной из основных тестовых функций для проверки эффективности многомерных методов безусловной минимизации, которые стартуют из начальной точки
, определяющей дно искривленного оврага. Поскольку линии уровня напоминают линии разреза банана, функцию Розенброка называют также «бананообразной» функцией. Она является одной из основных тестовых функций для проверки эффективности многомерных методов безусловной минимизации, которые стартуют из начальной точки ![]() . На рис. 1.4 и 1.5 отмечены: звездочкой – точка минимума
. На рис. 1.4 и 1.5 отмечены: звездочкой – точка минимума ![]() , кругом – начальная точка
, кругом – начальная точка ![]() , штриховой линией – дно оврага функции Розенброка. Поскольку начальная точка расположена на дальнем склоне оврага относительно точки минимума функции, то для достижения точки минимума метод оптимизации должен преодолеть искривленный овраг с одним поворотом, что является непростой задачей.
, штриховой линией – дно оврага функции Розенброка. Поскольку начальная точка расположена на дальнем склоне оврага относительно точки минимума функции, то для достижения точки минимума метод оптимизации должен преодолеть искривленный овраг с одним поворотом, что является непростой задачей.
|
|
|
Рис. 1.4. График функции Розенброка |
|
|
|
Рис. 1.5. Линии уровня функции Розенброка |
Только тот численный метод оптимизации, который сможет минимизировать функцию Розенброка из заданной начальной точки, может считаться эффективным для минимизации гладких функций.
| < Предыдущая | Следующая > |
|---|