07. Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование ряда
Теорема. Пусть ![]() на
на ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() .
.
Доказательство. Требуется доказать, что ![]() функция
функция ![]() непрерывна в точке
непрерывна в точке ![]() , т. е.
, т. е. ![]() . Зафиксируем произвольное
. Зафиксируем произвольное ![]() . Ввиду равномерной сходимости
. Ввиду равномерной сходимости ![]() . В частности,
. В частности, ![]() . По условию, при любом
. По условию, при любом ![]() функция
функция ![]() - непрерывная. Значит,
- непрерывная. Значит, ![]() . При выбранных
. При выбранных ![]() имеем:
имеем: ![]()
![]() , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Сумма равномерно сходящегося ряда, члены которого являются непрерывными функциями, есть непрерывная функция.
Доказательство. Применим предыдущую теорему к последовательности частичных сумм ряда.
Теорема. (почленное интегрирование ряда). Пусть ряд ![]() равномерно сходится к своей сумме
равномерно сходится к своей сумме ![]() на отрезке
на отрезке ![]() и все
и все ![]() . Тогда
. Тогда ![]()
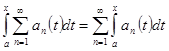 .
.
Доказательство. Обозначим при произвольном ![]() ,
, ![]() . Тогда
. Тогда ![]() - непрерывная функция и, т. к. по предыдущей теореме
- непрерывная функция и, т. к. по предыдущей теореме ![]() - непрерывная функция,
- непрерывная функция, ![]() - также непрерывная функция. Тогда
- также непрерывная функция. Тогда 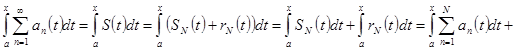
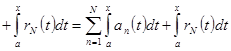 . Для доказательства теоремы достаточно доказать, что
. Для доказательства теоремы достаточно доказать, что 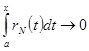 при
при ![]() , т. к., по определению,
, т. к., по определению, 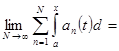
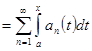 . Но
. Но ![]() . Поэтому при
. Поэтому при ![]()
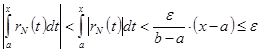 и требуемое утверждение доказано.
и требуемое утверждение доказано.
Замечание. Для функциональных последовательностей эта теорема формулируется следующим образом: Пусть ![]() на
на ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда 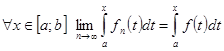 .
.
Теорема. (о почленном дифференцировании ряда).
Пусть:
1. ![]() ;
;
2. Ряд ![]() сходится на
сходится на ![]() (и пусть его сумма обозначена
(и пусть его сумма обозначена ![]() );
);
3. Ряд ![]() равномерно сходится на
равномерно сходится на ![]() .
.
Тогда ![]() или, иными словами,
или, иными словами, 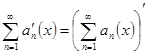 .
.
Доказательство. Обозначим ![]() - сумму ряда
- сумму ряда ![]() . Тогда
. Тогда ![]() - непрерывная на
- непрерывная на ![]() функция. Поэтому
функция. Поэтому ![]() существует ее интеграл от
существует ее интеграл от ![]() и он, по предыдущей теореме, равен
и он, по предыдущей теореме, равен 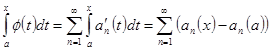
![]() . Значит,
. Значит, ![]() или
или 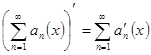 .
.
Замечание. Соответствующая теорема для последовательностей может быть сформулирована так: Пусть ![]() . Пусть
. Пусть ![]() ,
, ![]() и пусть
и пусть ![]() ,
, ![]() . Тогда
. Тогда ![]() , или
, или ![]() .
.
| < Предыдущая | Следующая > |
|---|