03. Интегральный признак сходимости. Сходимость ряда

Теорема. Пусть - непрерывная, неотрицательная, монотонно убывающая функция, определенная при . Тогда ряд и интеграл либо оба сходятся, либо оба расходятся.

Доказательство. Ввиду монотонности при всех выполняются неравенства . Интегрируя, получаем 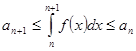. Тогда , или . Поэтому если сходится, то . Тогда и , ряд сходится.

Пусть теперь наоборот, известно, что ряд сходится. Тогда . Взяв произвольное выберем так, чтобы . Тогда . Значит, сходится.

 

Геометрическая иллюстрация теоремы.

- площадь под графиком на отрезке от 1 до . - площадь “верхней лестницы”, расположенной над графиком и - площадь “нижней лестницы”, под графиком.

 

Пусть ряд и интеграл сходятся. Тогда остаток ряда .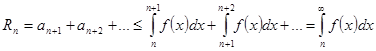

Теорема. Сходимость ряда .

Ряду соответствует функция . сходится при и расходится при . По доказанной теореме, ряд сходится при и расходится при .

 

 

 

< Предыдущая		Следующая >