3.2 Минимизация частично определенных функций

Пусть функция F(X1,…,Xn) частично (не всюду) определена. Если F не определена на P наборах из 0 и 1, то существует 2P возможностей для доопределения функции F. Полностью определенная функция G (X1,…,Xn) есть доопределение функции F, если G совпадает с F на тех наборах из 0 и 1, на которых F определена.

Задача минимизации частично определенной функции F сводится к отысканию такого доопределения G функции F, которое имеет простейшую (по числу букв ) минимальную форму.

Обозначим через F0(X1,…,Xn) и F1(X1,…,Xn) доопределения нулями и единицами соответсвенно частично определенной функции F(X1,…,Xn).

Теорема. Минимальная ДНФ частично определенной функции F(X1,…,Xn) есть дизъюнкция самых коротких импликант в сокращенной ДНФ доопределения F1(X1,…,Xn), которые в совкупности накрывают все конституенты единицы доопределения F0(X1,…,Xn).

Доказательство. Рассмотрим СДНФ некоторого доопределения G(X1,…,Xn) функции F(X1,…,Xn). Конституенты единицы, входящие в эту форму, войдут и в СДНФ доопределения F1. Поэтому любой простой импликант функции G будет совпадать с некоторым импликантом функции F1 или накрываться им. Самые короткие импликанты, накрывающие единицы функции F , есть импликанты функции F1. Доопределение F0 имеет минимальное количество конституент единицы в своей СДНФ, следовательно, и количество простых импликант функции F1 , потребных для накрытия этих конституент, будет наименьшим. ДНФ, составленная из самых коротких простых импликант в сокращенной ДНФ функции F1 , накрывающих все конституенты единицы функции F0 , будет самой короткой ДНФ, доопределяющей функцию F .

Так как единицы функции F1 составлены из единиц функции F и единиц на наборах, на которых F не определена, то построенная ДНФ, накрывая все единицы функции F0 ( а, следовательно, и все единицы функции F ) , совпадает с минимальной ДНФ некоторого доопределения G функции F .

Алгоритм минимизации частично определенных функций

В классе ДНФ

1. Строим СДНФ функции F0 .

2. Строим сокращенную ДНФ функции F1 .

3. С помощью матрицы покрытий коституент единицы функции F0 простыми импликантами функции F1 и решеточного выражения строим все тупиковые ДНФ (для некоторых доопределений функции F ) .

4. Среди полученных ТДНФ выбираем простейшие, они являются минимальными ДНФ ( для некоторых доопределений функции F ) .

Алгоритм минимизации частично определенных функций

В классе КНФ

Построение минимальных КНФ для частично определенной функции аналогично построению минимальных КНФ для всюду определенной функции.

Алгоритм минимизации частично определенных функций в классе нормальных форм аналогичен алгоритму минимизации в классе нормальных форм для всюду определенных функций.

Пример 1. В классе нормальных форм минимизировать частично определенную функцию F ( X, Y, Z, T ) = (1---010010-01--1)

Решение. Минимизируем функцию F в классе ДНФ.

1. Строим сокращенную ДНФ для доопределения единицами F1 функции F по таблице 3.9.

Таблица 3.9

X y z t

F F0 F1 `F H0 H1

0 0 0 0

0 0 0 1

0 0 1 0

0 0 1 1

0 1 0 0

0 1 0 1

0 1 1 0

0 1 1 1

1 0 0 0

1 0 0 1

1 0 1 0

1 0 1 1

1 1 0 0

1 1 0 1

1 1 1 0

1 1 1 1

1 1 1 0 0 0

- 0 1 - 0 1

0 0 0 1 1 1

1 1 1 0 0 0

0 0 0 1 1 1

1 1 1 0 0 0

0 0 0 1 1 1

- 0 1 - 0 1

0 0 0 1 1 1

1 1 1 1 1 1

- 0 1 - 0 1

1 1 1 0 0 0

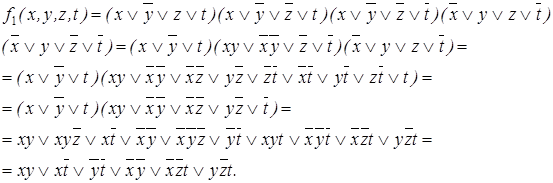
2. Строим матрицу покрытий коституент единицы в СДНФ для доопределения нулями F0 функции F с помощью построенной сокращенной ДНФ для F1 ( таблица 3.10).

Таблица 3.10

N	ПИ
1		+	+
2		+
3		+	+
4		+	+
5		+
6		+

3. По таблице строим решеточный многочлен

E = (2Ú4)(5Ú6)(3Ú4)(1Ú3)1 = 145 Ú 125 Ú 146 Ú 1236.

4. Строим все тупиковые ДНФ :

5. Из построенных тупиковых ДНФ выбираем минимальные :

Функции G1 и G3 есть минимальные доопределения функции F в классе ДНФ.

Минимизируем теперь функцию F в классе КНФ. Для этого проведем минимизацию функции `F в классе ДНФ Пусть H0 и H1 есть доопределение нулями и единицами соответственно функции `F .

Сокращенная ДНФ для

Матрица покрытия конституент единицы в СДНФ для H0 с помощью простых импликант в сокращенной ДНФ для H1 приведена в таблице 3.11.

Таблица 3.11

N	ПИ
1		+	+
2		+	+
3		+
4		+
5		+	+
6		+

3. Решеточное выражение E=5 (2 Ú 3 Ú5) 2 (1Ú 4)(1Ú 6) = 25(1Ú 46) = 125 Ú 2446.

4. Строим две тупиковые ДНФ:

Минимальная.

5. Функция есть минимальное доопределение функции F в классе КНФ.

Найденные МДНФ G1 , G3 и МКНФ являются минимальными доопределениями функции F в классе нормальных форм.

Техническая реализация минимальных форм для функции часто проще, а потому дешевле реализации ее СДНФ ( СКНФ ) . Следовательно, этап минимизации при конструировании логических схем является одним из важнейших.

Метод минимизирующих карт Карно

При построении сокращенных ДНФ для функций, зависящих от небольшого числа (не более 4) переменных, используется метод карт Карно. Построение карт Карно основано на свойствах булева куба.

Множество всех двоичных наборов длины N образует N-мерный булев или двоичный куб, который называют также единичным N-мерным кубом и обычно обозначают . Применяя геометрическую терминологию, наборы называют вершинами куба .

Расстоянием Хэмминга между вершинами и куба называется число оно равно числу координат, в которых наборы и отличаются друг от друга. Расстояние Хемминга является метрикой, а куб – метрическим пространством.

Наборы и из называются соседними если и противоположными если, т. е. соседние наборы различаются только в одной координате, а противоположные во всех координатах.

Символом обозначают множество т. е. множество всех наборов из , на которых функция обращается в 1.

Гранью единичного N-мерного куба называется множество Множество называется направлением, число K - рангом, а число N–K – размерностью грани . Кодом грани G= называется вектор длины N, в котором , а остальные координаты есть «–». Например =

(0–1–). Одномерные грани называются ребрами куба.

Обозначим множество векторов длины N с координатами из множества {0, 1, –} через Gn. На множестве Gn зададим частичный порядок, полагая если вектор может быть получен из путем замены некоторых (быть может, ни одной) координат набора , равных 0 и 1, на «–». Отношение между кодами граней G и H соответствует отношению между гранями. Положим равным числу прочерков в наборе и Тогда соответствует множеству ребер куба , – множеству граней куба , имеющих размерность K. Интервалом куба называется множество вида , где , – вершины из такие, что . Число называется размерностью интервала.

Если элементарная конъюнкция K является импликантой функции , то множество Nk всех наборов и из таких, что образует грань, содержащуюся в множестве Nf. Эта грань называется интервалом функции F, соответствующем импликанте K. Интервал функции F, не содержащийся ни в каком другом интервале функции F, называется максимальным интервалом. Максимальные интервалы функции F соответствуют ее простым импликантам.

В методе минимизирующих карт Карно функция задается прямоугольной таблицей, в которой наборы значений переменных на каждой из сторон прямоугольника расположены в коде Грея. Нахождение простых импликант сводится к выделению максимальных по включению прямоугольников, состоящих из единиц. Из прямоугольников, соответствующих граням максимальной размерности, находим коды максимальных интервалов. Считается, что каждая клетка таблицы является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали. Метод применим также и для не всюду определенных функций. В этом случае выделяются максимальные прямоугольники, содержащие хотя бы одну единицу и не содержащие нулей.

Пример 2. Таблица 3.12 представляет собой минимизирующую карту для функции с вектором значений Коды максимальных интервалов имеют вид (00-0), (000-), (--01), (-1-1), (110-). Сокращенная ДНФ имеет вид

Таблица 3.12 Таблица 3.13

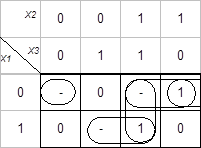
Пример 3. Таблица 3.13 представляет собой минимизирующую карту для частичной функции F, зависящей от трех переменных. Сокращенная ДНФ имеет вид

< Предыдущая		Следующая >