3.1. Минимизация нормальных форм

Минимальной ДНФ (МДНФ) функции F(X1, ... ,Xn) называется ДНФ, реализующая функцию F и содержащая минимальное число символов переменных по сравнению со всеми другими видами ДНФ, реализующими функцию F.

Если для всякого набора = (A1, ..., An) значений переменных условие G( )=1 влечёт , то функция G называется частью функции F (или функция F накрывает функцию G). Если при этом для некоторого набора = (C1, ..., Cn) функция G( )=1, то говорят, что функция G накрывает единицу функции F на наборе (или что G накрывает конституенту единицы функции F). Заметим, что конституента единицы функции F есть часть функции F, накрывающая единственную единицу функции F.

Элементарная конъюнкция K называется импликантом функции F, если для всякого набора =(A1, ..., An) из 0 и 1 условие K( )=1 влечет F( )=1.

Импликант K функции F называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции F.

Ясно, что всякий импликант функции F есть часть функции F.

Теорема. Всякая функция реализуется дизъюнкцией всех своих простых имликант (ПИ).

Доказательство. Пусть F(X1, ..., Xn) есть функция, а A = K1 v... v Km – дизъюнкция всех ее простых импликант. Пусть = (A1, ..., An) – произвольный набор длины N из 0 и 1.

Если A( ) = 1, то найдется дизъюнктивное слагаемое Ki ( ) = 1, что влечет F( ) = 1, ибо Ki есть импликант функции F.

Если F( ) = 1, то в СДНФ для функции F найдется элементарная конъюнкция K, равная на этом наборе единице. Один из простых имликантов Kj функции F получается выбрасыванием некоторых множителей из K и потому Kj( ) = 1, а тогда A( ) = 1.

Следовательно, F = A. Теорема доказана.

Сокращенная ДНФ функции F есть дизъюнкция всех простых импликант функции F. Всякая функция F реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Пусть A и B – произвольные формулы. Из свойств булевых операций вытекают следующие обратимые правила преобразования ДНФ:

1) – полное склеивание (развертывание);

2) – неполное склеивание;

3) – обобщенное склеивание;

4) – поглощение;

5) – идемпотентность ( удаление дублирующих членов).

Теорема ( Квайна ). Если в СДНФ функции F провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращения ДНФ функции F.

Доказательство. Пусть имеем сокращенную ДНФ функции F. Проведем все операции развертывания к каждому простому импликанту для получения недостающих переменных в каждом дизъюнктивном слагаемом сокращенной ДНФ. В полученном выражении из нескольких одинаковых дизъюнктивных слагаемых оставим только по одному экземпляру. В результате получим СДНФ функции F. Теперь, исходя из полученной СДНФ, в обратном порядке проведем операции добавления одинаковых дизъюнктивных слагаемых (с помощью правил идемпотентности), неполного склеивания и поглощения. В итоге получим исходную сокращенную ДНФ.

Алгоритм Квайна построения сокращенной ДНФ.

1. Получить СДНФ функции F.

2. Провести все операции неполного склеивания.

3. Провести все операции поглощения.

Пример 1. Построим сокращенную ДНФ для функции, приведенной в таблице 3.1.

Таблица 3.1

0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1

0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1

0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1

0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 1

1. Строим СДНФ функции F:

. Пронумеруем дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.

2. Проводим все операции неполного склеивания.

Первый этап склеивания в таблице 3.2.

После первого этапа склеиваний (и возможных поглощений) получаем, что

Пронумеруем дизъюнктивные члены в полученной ДНФ в порядке их следования от 1 до 15.

Второй этап склеиваний в таблице 3.3.

После второго этапа склеиваний и последующих поглощений получаем, что Это и будет сокращенной ДНФ для функции f, ибо дальнейшие склеивания невозможны.

Таблица 3.2

Слагаемые	Склеивание по	Результат
1,2	T
1,3	Z
1,6	X
2,4	Z
2,5	Y
3,4	T
3,7	X
5,9	X
6,7	Z
6,8	Y
7,10	Y
8,9	T
8,10	Z
9,11	Z	Xyt
10,11	T	Xyz

Таблица 3.3

Слагаемые	Склеивание по	Результат
1, 6	Z
2, 4	T
2, 8	X
3, 7	Z
8, 13	Y	X
10, 11	Z	X
12, 15	Z	Xy
13, 14	T	Xy

Метод Блейка

Метод Блейка для построения сокращенной ДНФ из произвольной ДНФ состоит в применении правил обобщенного склеивания и поглощения. Подразумевается, что правила применяются слева направо. На первом этапе производится операция обобщенного склеивания до тех пор, пока это возможно. На втором производится операция поглощения.

Пример 2. Построить сокращенную ДНФ по ДНФ D функции F(X,Y,Z), где

После первого этапа получаем:

После второго этапа получаем сокращенную ДНФ:

Алгоритм построения сокращенной ДНФ с помощью КНФ

(метод Нельсона)

Пусть F(X1, … , Xn) есть некоторая функция алгебры логики. Построим для F некоторую КНФ. Осуществим далее следующие преобразования.

1. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание. В результате получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ.

2. В полученном выражении удалим нулевые дизъюнктивные слагаемые.

3. В полученном выражении проведем все поглощения, а затем удалим дублирующие члены.

В результате проведенных операций получим сокращенную ДНФ функции F. Покажем это.

Для каждой элементарной дизъюнкции D в КНФ и каждой элементарной конъюнкции K в сокращенной ДНФ (сокр. ДНФ) существует некоторый множитель вида X из K, содержащийся в D, т. е.

" DÎ ДНФ " K Î сокр. ДНФ $ Xa Î K (XaÎ D).

Допустим противное: в КНФ существует элементарная конъюнкция D, в сокращенной ДНФ существует элементарная конъюнкция K, для которой всякий множитель вида Xa из K не входит в D. Не уменьшая общности возьмем для простоты

Положим X1 = A1, …, Xk=Ak, Xk+1 = Ck+1 ¹ Ak+1, …, Xr = Cr ¹ Ar. Тогда K(A1, …, Ak) = 1, и потому F (A1, …, Ak, Ck+1, …, Cr ) = 1. С другой стороны, D(Ck+1,…, Cr) = 0, и потому F (A1, …, Ak, Ck+1, …, Cr ) = 0. Противоречие.

Пусть по-прежнему для простоты произвольный простой импликант K из сокращенной ДНФ равен . Тогда элементы попадут в не менее чем K скобок из КНФ. Если допустим, что этого нет, то при перемножении скобок из КНФ не получим дизъюнктивного слагаемого, которое содержало бы множители , а потому, строя из результата перемножения сокращенную ДНФ вычеркиванием лишних сомножителей, не получим простого импликанта K.

Так как содержатся в K разных скобках КНФ, а всякая другая скобка, отличная от указанных K скобок, содержит хотя бы один элемент вида X из K, то при раскрытии скобок имеем простой импликант K. После проведения всех операций поглощения и удаления дублирующих множителей, останутся только простые импликанты из сокращенной ДНФ, ибо если предположить наличие в результате хотя бы одного дизъюнктивного слагаемого, отличного от всех простых импликантов сокращенной ДНФ, то можно подобрать такие значения переменных функции F, на которых все простые импликанты примут значение 0, а это дополнительное слагаемое – значение 1, чего быть не может.

Пример 3. Построим сокращенную ДНФ этим способом для функции

F = (1111010010101111) из примера 1 :

Сокращенная ДНФ для функции

Что, естественно, совпадает с результатом примера 1.

Пример 4. Построить сокращенную ДНФ по заданной КНФ

После раскрытия скобок имеем:

После второго этапа получаем сокращенную ДНФ:

Тупиковой ДНФ ( ТДНФ) функции F называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции F.

Теорема. Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ.

Доказательство. В МДНФ входят только простые импликанты, иначе некоторые множители в непростом имликанте можно удалить в противоречие с минимальностью исходной ДНФ. В МДНФ нет лишних импликант, иначе исходная ДНФ не является минимальной.

Вывод. Для получения МДНФ функции F необходимо построить все ТДНФ функции F и выбрать из них те, которые содержат минимальное число букв.

Построение всех тупиковых ДНФ.

Пусть F(X1, …, Xn) есть функция алгебры логики.

1. Построим СДНФ функции F, и пусть P1, P2, …,Pn есть ее коституенты единицы).

2. Построим сокращенную ДНФ функции, F и пусть K1, K2, …, Km – ее простые импликанты.

3. Построим матрицу покрытий простых импликант функции F ее конституентами единицы (табл. 3.4), полагая, что

+, если каждый множитель в Ki является множителем в Pj; (Pj есть Aij= часть для Ki ); Æ в противном случае.

Таблица 3.4

P1 P2 … Pj …Pn

A11 a12 … a1J …a1N

A21 a22 … a2J … a2N

Ai1 ai2 … aij … ain

Am1 am2… amj … amn

4. Для каждого столбца J ( 1 £ J £ N ) найдем множество Ej всех тех номеров I строк, для которых Aij = 1. Пусть Составим выражение Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …,M и с операциями & и Ú .

5. В выражении A раскроем скобки, приведя выражение A к равносильному выражению где перечислены все конъюнкции элементы которой взяты из скобок 1,2,…,N соответственно в выражении A.

6. В выражении B проведем все операции удаления дублирующих членов и все операции поглощения. В результате получим дизъюнкцию элементарных конъюнкций C.

Утверждение. Каждая элементарная конъюнкция I1&I2&…&Ir в С дает ТДНФ для F . Все ТДНФ для функции F исчерпываются элементарными конъюнкциями в выражении С.

Пример 5. Сокращенная ДНФ для функции F = (1111010010101111) имеет вид

Для функции F построим все минимальные ДНФ.

1. Строим матрицу покрытий (таблица 3.5).

Таблица 3.5

Конституенты единицы функции F

ПИ

X `X `X `X `X X X X X X X

Y `Y `Y `Y y `Y `Y y y y y

Z `Z z z `Z `Z z `Z `Z z z

T t `T t t `T `T `T t t t

x y

`X`Y

`Y`T

x`T

`X`Z t

y`Z t

+ + + +

+ +

2. Строим решеточное выражение (по столбцам таблицы).

E = (2Ú3)(2Ú5)(2Ú3)2(5Ú6)(3Ú4)(3Ú4)(1Ú4)(1Ú6)(1Ú4)(1) = (2Ú3)(2Ú5)(5Ú6)(3Ú4)(1Ú4)(1Ú6)12 = (5Ú6)(3Ú4)(1)(2) = 1235Ú1245Ú1236Ú1246.

3. Строим все тупиковые ДНФ функции F:

простые импликанты 1,2,3,5;

простые импликанты 1,2,4,5;

простые импликанты 1,2,3,6;

простые импликанты 1,2,4,6.

4. Все найденные ТДНФ являются минимальными ДНФ.

Алгоритм минимизации функций в классе ДНФ

1. Строим СДНФ функции F.

2. Строим сокращенную ДНФ функции F.

3. С помощью матрицы покрытий и решеточного выражения строим все ТДНФ функции F.

4. Среди построенных ТДНФ выбираем все минимальные дизъюнктивные нормальные формы функции F.

Алгоритм минимизации функций в классе КНФ

Чтобы построить все минимальные КНФ (МКНФ) функции F, следует построить все МДНФ функции `F и взять от каждой из них отрицание, для чего заменить знаки & на Ú , а Ú на & ( сохранив первоначальное распределение скобок) и над каждой буквой поставить знак отрицания. Полученные КНФ для функции F будут минимальными. В самом деле, если бы для F существовала КНФ с меньшим числом букв, то ее отрицание дало бы для `F ДНФ с меньшим числом букв, чем в любой из минимальных ДНФ для `F. Противоречие с их минимальностью.

Алгоритм минимизации функций в классе нормальных форм

Пусть F – функция алгебры логики.

1. Строим все МДНФ функции F.

2. Строим все МКНФ функции F.

3. Из построенных минимальных форм выбираем простейшие ( по числу букв).

Пример 6. В классе нормальных форм минимизировать функцию F=(01011110).

1. Строим СДНФ для функции F :

2. Строим сокращенную ДНФ функции F:

3. Строим матрицу покрытий (таблица 3.6).

Таблица 3.6

ПИ

`X`Y z `X y z x`Y`Z x`Y z x y`Z

`X z

`Y z

X`Y

x`Z

+ +

Решеточное выражение E = ( 1 Ú 2 ) 1 (3 Ú 4 ) 4 = 134 Ú 124.

4. Строим все тупиковые ДНФ функции F :

5. Обе построенные ТДНФ являются минимальными.

6. Повторяем эти этапы для функции `F.

СДНФ :

Сокращенная ДНФ :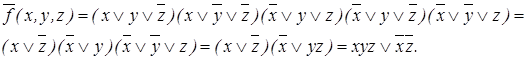

Строим матрицу покрытий (таблица 3.7).

Таблица 3.7

ПИ

X`y`z `x y`z x y z

`x`z

X y z

+ +

Решеточный многочлен E = 112 = 12. Единственная тупиковая ДНФ (она же минимальная) для функции Минимальная КНФ функции Из построенных МДНФ и МКНФ выбираем простейшую