06. ОДУ первого порядка с разделяющимися переменными
Если в результате каких-либо преобразований ДУ первого порядка ![]() удалось привести к виду
удалось привести к виду
![]() , (3)
, (3)
То говорят, что это дифференциальное уравнение является уравнением с разделяющимися переменными (переменные «разделились» по разные стороны от знака равенства). Тогда решение этого ДУ может быть найдено в квадратурах:
![]()
![]() , где
, где ![]() - первообразные функций
- первообразные функций ![]() И
И ![]() соответственно.
соответственно.
Пример:
Найти общее решение ДУ: ![]()
Представим производную как отношение дифференциалов: ![]()
![]()
Разнесем слагаемые по разные стороны от знака равенства:
![]() , откуда
, откуда 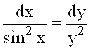 .
.
Получили уравнение с разделяющимися переменными, откуда, интегрируя правую и левую части, получим:
 . Знак постоянной С выбран отрицательным для того, чтобы можно было чуть упростить решение, отбросив знак минус.
. Знак постоянной С выбран отрицательным для того, чтобы можно было чуть упростить решение, отбросив знак минус.
 .
.
Это выражение и является общим решением ДУ.
Пример:
Найти решение задачи Коши для ДУ:
![]() с начальным условием
с начальным условием ![]() .
.
![]()
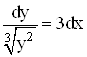
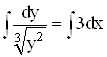
![]()
![]()
![]()
Подставим в полученное выражение начальное условие:
![]()
![]()
Решение задачи Коши: ![]()
| < Предыдущая | Следующая > |
|---|