04. Общие понятия и положения теории дифференциальных уравнений

В математике часто встречаются уравнения, в которые, кроме неизвестной переменной (или нескольких переменных) входит неизвестная функция и ее производные (частные производные). Такие уравнения называются Дифференциальными уравнениями.

Если функция зависит от одной переменной, то такое уравнение называют обыкновенным дифференциальным уравнением – ОДУ. Если же функция зависит от нескольких переменных, то такое уравнение называют (дифференциальным) уравнением в частных производных – ДУвЧП. Исторически дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.

В данном пособии будут рассматриваться обыкновенные дифференциальные уравнения.

Уравнение вида

(1)

Называется ОДУ n-го порядка из-за того, что максимальный порядок производной в этом уравнении равен n.

Пример: второй закон Ньютона представляется в виде ОДУ второго порядка

,

Где где m — масса тела, x — его координата, F(x, t) — внешняя сила, действующее на тело с координатой x в момент времени t, вторая производная x по времени t. Решением этого уравнения является траектория движения тела под действием указанной силы.

Общим решением дифференциального уравнения называют функцию , которая при подстановке в дифференциальное уравнение вида обращает его в тождество. Постоянные являются константами интегрирования.

Пример:

Рассмотрим уравнение . Это ОДУ первого порядка. Очевидно, что функция, например, Является решением этого уравнения (это легко проверить, просто посчитав производную функции). Но решением будет также и функция и . Аналогично можно показать, что любое решение вида , где С – произвольная постоянная, является решением данного уравнения. Функции такого вида и являются общим решением ДУ .

Частным решением ДУ называют функцию вида , которая при подстановке ее в дифференциальное уравнение вида обращает уравнение в тождество.

Пример:

Все функции y1, y2 и y3 из предыдущего примера являются частными решениями уравнения .

Таким образом, можно сказать, что общее решение ДУ это совокупность всех его частных решений.

Задачей Коши или Начальной задачей для ОДУ n-го порядка называется совокупность самого дифференциального уравнения и начальных условий, т. е. значений функции и ее производных до n-1 порядка включительно, заданных в одной точке:

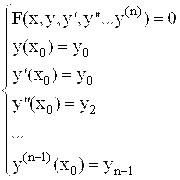(2)

При определенных, достаточно общих ограничениях на функцию F (которые здесь оговаривать не будем) задача Коши имеет решение, и оно является единственным.

Число начальных условий задачи Коши должно соответствовать порядку дифференциального уравнения для однозначного нахождения всех неизвестных постоянных интегрирования . Решение задачи Коши является частным решением ОДУ.

Пример: поставлена задача Коши для ОДУ первого порядка.

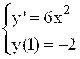
Общее решение этого ОДУ, как показано выше, имеет вид . Подставляя в него начальное условие, получаем: , откуда находим значение постоянной . Таким образом, решение задачи Коши примет вид .

На рисунке представлены несколько графиков, соответствующих четырем частным решениям некоторого ОДУ. Допустим, надо найти решение задачи Коши с начальными условиями , т. е. изо всей совокупности частных решений (общее решение) надо выбрать то, график которого проходит через точку с координатами (2,3). Очевидно, что это будет график, выделенный синим цветом.

< Предыдущая		Следующая >