03. Контрольные задания
Задача 1. Дифференциальные уравнения с разделяющимися переменными. Найти общее решение.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. 
9. ![]()
10. ![]()
Задача 2. Однородные дифференциальные уравнения. Найти общее решение.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. 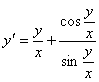
10. ![]()
Задача 3. Линейные дифференциальные уравнения первого порядка
- 1.
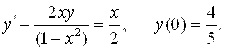
Задача 4. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Задача 5. Исследовать сходимость положительного ряда, применяя какой – либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный):

Задача 6. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости:

Задача 7. (Комбинаторный метод вычисления вероятностей в классической схеме).
Варианты 1, 2
В магазин поступило N телевизоров. Из них K Имеют скрытые дефекты. Покупателю для выбора наудачу предложено L телевизоров. Какова вероятность того, что все предложенные покупателю изделия не содержат дефектов?
1. N=30, K=3, L=2.
2. N=20, K=2, L=3.
Варианты 3,4
Из партии, содержащей N изделий, среди которых K бракованных, наудачу извлекают M изделий для контроля. Найти вероятности следующих событий: А={в полученной выборке ровно L бракованных изделий}, B={в полученной выборке нет бракованных изделий}.
3. N=10, K=3, L=1, M=4.
4. N=12, K=3, L=2, M=5
Варианты 5,6
Имеются два ящика с деталями. В первом N Деталей, из них M годных. Во втором ящике N Изделий, из них M годных. Сборщик наудачу выбрал по одной детали из каждого ящика. Найти вероятность того, что обе выбранные детали годные. Какова вероятность того, что обе выбранные детали бракованные?
5. N=12, M=8, N=8, M=7.
6. N=14, M=10, N=6, M=4.
Варианты 7,8
Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если:
7. число мест равно 8.
8. число мест равно 12.
Варианты 9,10
Из урны, содержащей M+N шаров, из которых M белых и N черных, на удачу отбирают K Шаров и откладывают в сторону. Найти вероятности следующих событий: A={все отложенные шары белые}, B={среди отложенных шаров ровно L белых}.
9. M=10, N=6, K=5, L=3.
10. M=8, N=12, K=6, L=4.
Задача 8 (Формула полной вероятности и формула Байеса)
Варианты № 1, 2
В сборочный цех поступает некоторая деталь с трёх станков-автоматов. Среди изделий первой линии ![]() % Стандартных, у второй линии
% Стандартных, у второй линии ![]() %,
%, ![]() % - У третьей линии. Объём продукции первой линии
% - У третьей линии. Объём продукции первой линии ![]() %, второй линии
%, второй линии ![]() %. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная.
%. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная.
1. ![]() =98% ,
=98% , ![]() =95%
=95% ![]() =92% ,
=92% , ![]() =40% ,
=40% , ![]() =30%.
=30%.
2. ![]() =97%,
=97%, ![]() =96%,
=96%, ![]() =95% ,
=95% , ![]() =45% ,
=45% , ![]() =35%.
=35%.
Варианты № 3, 4
В тире имеется три вида винтовок: ![]() - первого типа,
- первого типа, ![]() - второго типа,
- второго типа, ![]() - третьего типа. Вероятность попадания в цель из винтовок первого типа
- третьего типа. Вероятность попадания в цель из винтовок первого типа ![]() , второго типа
, второго типа ![]() , третьего типа
, третьего типа ![]() . После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?
. После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?
3. ![]() =3,
=3, ![]() =4,
=4, ![]() =3,
=3, ![]() =0.9,
=0.9, ![]() =0.85,
=0.85, ![]() =0.65.
=0.65.
4. ![]() =1,
=1, ![]() =3,
=3, ![]() =5,
=5, ![]() =0.65,
=0.65, ![]() =0.7,
=0.7, ![]() =0.75.
=0.75.
Варианты № 5,6
В магазин поступают телевизоры с трёх заводов. С первого завода поступает ![]() % телевизоров со скрытыми дефектами,
% телевизоров со скрытыми дефектами, ![]() % со второго завода и
% со второго завода и ![]() % с третьего завода. Какова вероятность того, что в магазин привезут исправный телевизор, если известно, что с первого завода поступило телевизоров
% с третьего завода. Какова вероятность того, что в магазин привезут исправный телевизор, если известно, что с первого завода поступило телевизоров ![]() , со второго
, со второго ![]() , с третьего
, с третьего ![]() ?
?
5. ![]() =10%,
=10%, ![]() =5%,
=5%, ![]() =6%,
=6%, ![]() =3,
=3, ![]() =3,
=3, ![]() =4.
=4.
6. ![]() =15%,
=15%, ![]() =10%,
=10%, ![]() =15%,
=15%, ![]() =5,
=5, ![]() =3,
=3, ![]() =2.
=2.
Варианты № 7,8
В ящике N теннисных мячей. Из них игранных M. Для первой игры наудачу взяли два мяча и после игры их положили обратно. Для второй игры также наудачу взяли два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
7. N=10, M=2.
8. N=12, M=4.
Варианты № 9,10
Три стрелка произвели по выстрелу в одну и ту же мишень. Вероятность попадания у них соответственно Р1, р2, р3. В мишени оказались две пробоины. Определите вероятность промаха N-го стрелка.
9. р1 =0.5, р2=0.7, р3 =0.9, N=1.
10. р1 =0.6, р2=0.8, р3 =0.9, N=2.
Задача №6 Дискретные случайные величины.
Составить закон распределения дискретной случайной величины Х. Записать функцию распределения, построить её график. Вычислить числовые характеристики М(Х), D(Х), S(Х)).
Варианты №1,2,3,4
Х-число отказавших элементов в одном опыте с устройством, состоящим из N Независимо работающих элементов. Вероятность отказа каждого элемента Р.
1. N=3, P=0.1.
2. N=4, P=0.15.
3. N=3, P=0.15.
4. N=4, P=0.2.
Варианты №5,6,7
В партии K% бракованных изделий. Наудачу отобрано N Изделий. Х- число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону:
5. K=15%, N=4.
6. K=10%, N=5.
7. K=20%, N=3.
Варианты №8,9,10
В партии из N деталей имеется M стандартных. Наудачу отобрали K деталей. Х-число стандартных деталей среди отобранных.
8. N=10, M=8, K=3.
9. N=9, M=7, K=3.
10. N=12, M=10, K=3.
Задача № 7 (Выборка, выборочные характеристики)
Из изучаемой налоговыми органами обширной группы населения случайным образом отобраны 10 человек и собраны сведения об их доходах за истекший год в тысячах рублей: Х1, х2,…, х10. Найти выборочное среднее, исправленную выборочную дисперсию. Считая распределение доходов в группе нормальным и принимая в качестве его параметров выборочные характеристики, определить, какой процент населения имеет годовой доход, превышающий 70 тыс. рублей.
|
№ вар |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
|
1 |
50 |
40 |
60 |
80 |
40 |
50 |
60 |
120 |
70 |
50 |
|
2 |
45 |
65 |
85 |
45 |
55 |
65 |
95 |
75 |
65 |
55 |
|
3 |
80 |
70 |
60 |
50 |
70 |
90 |
50 |
60 |
70 |
100 |
|
4 |
65 |
55 |
45 |
65 |
85 |
55 |
45 |
65 |
100 |
80 |
|
5 |
50 |
60 |
70 |
100 |
80 |
70 |
60 |
50 |
70 |
90 |
|
6 |
100 |
40 |
80 |
90 |
50 |
60 |
80 |
70 |
70 |
50 |
|
7 |
100 |
50 |
80 |
90 |
100 |
130 |
55 |
60 |
100 |
80 |
|
8 |
70 |
40 |
45 |
90 |
110 |
60 |
50 |
40 |
110 |
90 |
|
9 |
80 |
110 |
90 |
80 |
70 |
60 |
60 |
50 |
65 |
50 |
|
10 |
90 |
40 |
60 |
40 |
80 |
65 |
90 |
70 |
50 |
60 |
| < Предыдущая | Следующая > |
|---|