07. О статической и геометрической вероятности

Относительная частота события А - это отношение числа испытаний, в которых событие фактически появилось (благоприятствующих А) к общему числу проведенных испытаний: .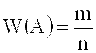

Если классическая вероятность вычисляется до опыта, то относительная частота - после опыта. Конечно, при увеличении количества испытаний в серии на 1 W(A) меняется - хотя бы потому, что на единицу изменяется знаменатель дроби. Тем не менее, с увеличением n величина W(A) приближается к некоторому числу, которое называют статистической вероятностью события А.

Заметим, что когда в задаче говорится, что “вероятность поражения стрелком мишени равна 0,7”, то речь идет о вероятности, вычисленной статистически.

Бывают задачи, когда множества всех элементарных исходов и благоприятствующих исходов невозможно пересчитать. В этих задачах иногда удается выразить вероятность события как отношение либо длин, либо площадей, либо объемов. Например, если считать, что попадания в круглую мишень происходят равномерно по площади всей мишени, а диаметр центра мишени в 5 раз меньше диаметра самой мишени, то вероятность попадания в центр (при условии попадания в мишень) равна отношению площадей центра мишени и всей мишени:

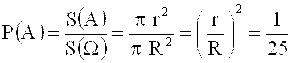
В этом случае количество вариантов, благоприятствующих А, бесконечно, но и общее число вариантов исхода испытания бесконечно, т. е. формулы классической или статистической вероятности неприемлемы.

Вероятность, определяемую как отношение длин, площадей, объемов, называют геометрической вероятностью.

< Предыдущая		Следующая >