21. Нормальный закон распределения и его характеристики

Нормальный (гауссовский) закон распределения задается плотностью распределения по формуле

, - ¥ < x < +¥

Числа а Î R и s > 0 называются параметрами нормального закона. Нормальный закон с такими параметрами обозначается N(a, s).

При а = 0 функция f(x) четная ( f(-x) = f(x) ) , ее график симметричен относительно оси OY, и поэтому среднее значение М(Х) = 0. График f(x) для закона N(a, s) получается из графика f(x) для N(0,s) сдвигом на а единиц вправо ( это известно из курса средней школы ), поэтому в общем случае М(Х) = а для нормального закона.

Дисперсия же вычисляется по формуле D(X) =s2.

Пример. Случайная величина Х распределена по нормальному закону с плотностью вероятности

Найти А, М (Х), D(X), P(-3<X<3).

Т. к. , то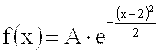

Показатель экспоненты приравняем к , откуда а = 2 , s = 1 . Числовой коэффициент 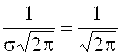Должен быть равен А, следовательно,

, M (X) = a = 2, D(X) = s 2 = 1.

P (-3 < X < 3) = F(3) - F(-3) = =

Этот интеграл не вычисляется в элементарных функциях, его численное значение можно найти по таблицам.

В большинстве учебников имеются таблицы для вычисления функций

Ф(х) = 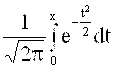или Ф1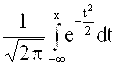(х) = = + Ф(х)

Ф(х) - нечетная функция, т. е. Ф(-х) = - Ф(х). В общем случае

Р(x1 < X < x2) = ,

Где а и s - параметры нормального закона. Следовательно, для данного примера

P(|X| < 3) = Ф1(1) - Ф1(-5) = Ф(1) - Ф(-5) = Ф(1) + Ф(5) =

= 0,3413 + 0,5 = 0,8413.

< Предыдущая		Следующая >