20. Случайные величины непрерывного типа

Если возможные значения случайной величины сплошь заполняют некоторый промежуток <a, b> Ì R (быть может, и всю Ось) , то табличный способ задания случайной величины непригоден. Такая случайная величина называется случайной величиной непрерывного типа. Ее функция распределения F(x) будет непрерывна. Напомним, что F(- ¥ ) = 0 , F(+ ¥ ) = 1 , F(x) - монотонная неубывающая функция. Производная такой функции F(x) будет функцией неотрицательной. Она называется плотностью распределения вероятностей или дифференциальной функцией распределения вероятностей. Ее обозначение .

Часто по условию задачи задают именно плотность распределения, зная которую можно вычислить и (интегральную) функцию распределения ( по формуле Ньютона - Лейбница ):

F(x) = F(x) - F(- ¥ ) =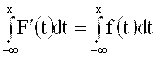

Заметим, что f(x) - не обязательно непрерывная функция, она допускает в отдельных точках разрывы 1-го рода.

Итак, f(x) - неотрицательная кусочно-непрерывная функция, причем, согласно одному из свойств F(x),

F(+ ¥ ) =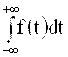= 1

Последнее равенство, называемое условием нормировки f(x), показывает, что f(x) - не любая неотрицательная функция: площадь между графиком плотности распределения и осью абсцисс должна быть равна 1.(Для дискретной случайной величины условием нормировки являлось равенство ).

Для непрерывных случайных величин справедливы равенства F(b) - F(a) = P(a £ X < b) = P(a < X < b) = P(a < X £ b) = = P(a £ X £ b) = .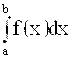

М(Х) и D(X) определяются формулами

M(X) =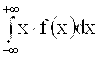, D(X) =.

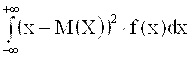Вычислительная формула для D(X):

D(X) = M(X2) - (M(X))2 = 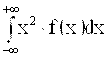- (M(X))2.

< Предыдущая		Следующая >