14. Другие формулы вычисления вероятностей для схемы Бернулли

Хотя формула Бернулли и является точной, она не всегда удобна. Например, при 100 бросках монеты

,

И вычисление точного ответа затруднительно. Формула Бернулли приемлема для вычислений, если число испытаний не превышает 10-15. При больших n используют либо формулу Лапласа, либо формулу Пуассона.

Формула Лапласа ( локальная теорема Лапласа )

, ,

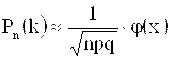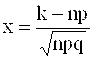
Тем точнее, чем больше n. Здесь n, k, p, q - те же величины, что и в формуле Бернулли. Функция j(x) четная: j(-x) = j(x) . Она быстро убывает: считают, что при x > 4 j(x) = 0. Таблица, позволяющая вычислять значения функции j(x), имеется во всех учебниках и задачниках по теории вероятностей. Впрочем, можно не иметь таблицы, а иметь калькулятор, вычисляющий экспоненту (функцию ех).

Пример 1. Вероятность выпадения ровно 50 “орлов” при 100 бросках монеты Р100(50) вычислим по формуле Лапласа. Здесь n = 100 ,k = 50 ,p=0,5, q = 0,5 , k - np = 0 , и

.

Пример 2. Найти вероятность выпадения от 47 до 57 “орлов” при 100 бросках монеты.

При решении подобных задач ( при n > 15 ) используют интегральную теорему Лапласа: вероятность Рn(k1,k2) появления события в n испытаниях от k1 до k2 раз

Здесь n, p, q те же, что и в примере 1 : n=100 , p = q =0,5 , k1=47 , k2 = 57 .

Функция F вычисляется с помощью таблиц ( см. приложение ).

Функция Ф(x) нечетная: Ф(-х) = - Ф(х) . При х > 5 считают, что Ф(х) = 0,5.

Итак, Р100(47,57) = Ф(1,4) + Ф(0,6). По таблице Ф(1,4) = 0,4192, Ф(0,6) = 0,2257 , поэтому Р100(47,57) = 0,6449.

При небольших значениях вероятности p ( меньших 0,1 ) и больших значениях n более точный результат дает другая приближенная формула - формула Пуассона

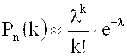, l = np

L называется параметром распределения Пуассона, а сама формула выражает “закон редких явлений” (т. к. p мало).

Пример 3. Первый черновой набор “Методических указаний” на 50 страницах содержит 100 опечаток. Какое из событий вероятнее: на наудачу взятой странице нет опечаток, 1 опечатка, 2 опечатки, 3 опечатки?

Вероятность того, что данная опечатка попадет на наудачу взятую страницу равна 1/50 = 0,02 , число испытаний ( опечаток ) n = 100 . Поскольку p мало, воспользуемся формулой Пуассона с параметром l = np = 2 . Вероятность того, что опечаток нет

( т. к. 0! = 1 )

Другие вероятности

, .

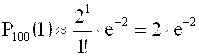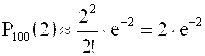
Как видим, наибольший коэффициент при е-2 у Р100(1) и Р100(2).

Ответ: наиболее вероятны 1 или 2 опечатки, их вероятность .

< Предыдущая		Следующая >