16. Линейные операторы и их матрицы

Линейным оператором в линейном пространстве называется всякое отображение Пространства В себя, обладающее линейными свойствами

и .

Например, в пространстве трехмерных арифметических векторов, проектирование на плоскость , задаваемое по правилу

,

Является линейным оператором, что проверяется непосредственно по определению. Единичный оператор , реализующий тождественное отображение, также является линейным оператором.

Множество элементов линейного пространства , которые являются образами векторов из области определения оператора, называют образом оператора И обозначают .

Ядром линейного оператора называют множество элементов линейного пространства , образом которых является нулевой элемент. Ядро оператора обозначают .

Непосредственно из определений следует, что и образ, и ядро оператора являются линейными подпространствами. При этом размерность образа оператора называют рангом оператора И обозначают .

Размерность ядра оператора называют дефектом оператора и обозначают . Доказывается, что сумма ранга и дефекта оператора равна размерности пространства, в котором действует оператор:

.

Пусть - произвольный линейный оператор в -мерном линейном пространстве с некоторым фиксированным базисом . Разложим преобразованные векторы по исходному базису:

.

Квадратная матрица, составленная из коэффициентов этого разложения

,

Называется матрицей оператора В заданном фиксированном базисе.

По теореме о единственности разложения векторов по базису, каждому линейному оператору соответствует единственная матрица оператора в фиксированном базисе. Отметим, что, выбрав другой базис в линейном пространстве, мы получили бы другую матрицу для того же оператора.

Обратно, если задана некоторая произвольная квадратная матрица и фиксирован некоторый базис , то этой матрице соответствует единственный линейный оператор , действующий по правилу , где- столбцы координат векторов в указанном базисе.

Таким образом, между линейными операторами и матрицами имеется взаимно однозначное соответствие для любого фиксированного базиса. Ранг линейного оператора и ранг матрицы оператора всегда совпадают, причем независимо от выбора базиса в исходном векторном пространстве .

Число называется собственным значением, а ненулевой вектор - соответствующим этому числу собственным вектором линейного оператора, если они связаны между собой соотношением

.

В -мерном линейном пространстве с некоторым базисом векторное равенство Равносильно матричному равенству . Для того чтобы найти собственные векторы, следует найти ненулевые решения однородной системы уравнений

.

Такие решения существуют только в том случае, когда ранг матрицы строго меньше числа неизвестных . Отсюда следует, что . Уравнение

Относительно неизвестного называют характеристическим уравнением линейного оператора, а многочлен

Степени называют характеристическим многочленом оператора.

Как известно, многочлен степени имеет ровно вещественных или комплексных корней с учетом их кратности. Таким образом, решив уравнение , мы получим систему чисел .

Некоторым из этих чисел Соответствуют бесконечные множества ненулевых собственных векторов, выделяемые из общего решения однородной системы уравнений . Множество всех таких собственных чисел называют спектром линейного оператора. Доказывается, что спектр линейного оператора не зависит от выбора в нем базиса.

Найдем, для примера, собственные значения и собственные векторы линейного оператора , заданного с помощью следующей матрицы оператора

.

Составим характеристическое уравнение оператора

.

Раскрывая определитель по правилу Саррюса и приводя подобные члены, получим кубическое уравнение относительно неизвестного

.

Это уравнение имеет три вещественных корня, которые обычно нумеруют в порядке убывания с учетом кратности

.

Для каждого значения составляются однородные системы уравнений относительно неизвестных :

.

Для однородная система имеет вид

.

Преобразуем матрицу коэффициентов нашей системы в соответствии с прямым ходом метода Гаусса

.

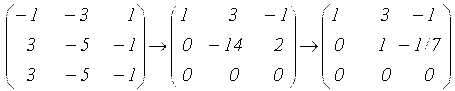Ранг преобразованной матрицы равен двум, поэтому имеем два базисных неизвестных и одно свободное неизвестное . Полагаем свободное неизвестное равным произвольной постоянной: . Неизвестные Находим из системы уравнений, соответствующей преобразованной матрице, в виде

.

Отбрасывая из общего решения системы нулевое решение, бесконечное множество собственных векторов линейного оператора обычно записывают в строку в

Виде , или в столбец в виде .

Здесь символом Обозначена переменная, принимающая возможные значения собственных векторов, отвечающих собственному значению два; буквой - произвольная постоянная, принимающая любые ненулевые вещественные значения, - один из удобных собственных векторов, записанный в строку и полученный из общего решения при .

Аналогично, составляются однородные системы уравнений для двух других корней характеристического уравнения. Эти системы исследуются по методу Гаусса. В нашем случае обе системы имеют нетривиальные решения, что позволяет получить множества собственных векторов, отвечающих этим числам, в следующем виде:

, .

< Предыдущая