15. Примеры использования метода Гаусса
Пример. Решим методом Гаусса следующую систему уравнений:
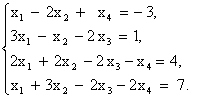
Выпишем расширенную матрицу этой системы и выполним ее элементарные преобразования по методу Гаусса. Умножим первую строку последовательно на числа 3, 2, 1 и вычтем результаты из второй, третьей и четвертой строк:
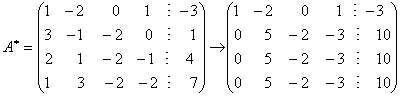
Вычтем теперь последовательно из третьей и четвертой строк вторую строку, а вторую строку разделим на число 5. Мы получили ступенчатую матрицу![]() , соответствующую этапу прямого хода метода Гаусса
, соответствующую этапу прямого хода метода Гаусса
 .
.
Примем за базисные неизвестные ![]() , а за свободные неизвестные
, а за свободные неизвестные ![]() . Отбросив в ступенчатой матрице
. Отбросив в ступенчатой матрице![]() нулевые строки, оставим в системе уравнений слагаемые с базисными неизвестными в левых частях уравнений, а слагаемые со свободными неизвестными перенесем со знаком минус в правые части уравнений:
нулевые строки, оставим в системе уравнений слагаемые с базисными неизвестными в левых частях уравнений, а слагаемые со свободными неизвестными перенесем со знаком минус в правые части уравнений:
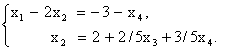
Полученная система имеет единственное решение относительно базисных неизвестных ![]() при любых значениях свободных неизвестных
при любых значениях свободных неизвестных ![]() . Подставляя выражение для
. Подставляя выражение для ![]() в первое уравнение системы, получим окончательно общее решение неоднородной системы в виде:
в первое уравнение системы, получим окончательно общее решение неоднородной системы в виде:
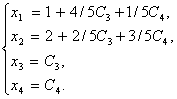
Запишем общее решение неоднородной системы, используя ее частное решение и фундаментальную систему решений, соответствующего однородного уравнения. Полагая в общем решении неоднородного уравнения, вектор произвольных постоянных ![]() равным нулевому вектору
равным нулевому вектору![]() , получим частное решение неоднородной системы в виде
, получим частное решение неоднородной системы в виде
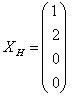 .
.
Далее положим в общем решении  соответствующего однородного уравнения вектор произвольных постоянных
соответствующего однородного уравнения вектор произвольных постоянных ![]() равным последовательно векторам канонического базиса
равным последовательно векторам канонического базиса ![]() ,
, ![]() . В результате получим фундаментальную систему решений в виде
. В результате получим фундаментальную систему решений в виде 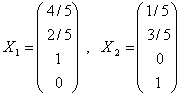 .
.
Окончательно, общее решение исходного неоднородного уравнения представляется в виде
 .
.
С помощью метода Гаусса можно эффективно вычислять обратную матрицу ![]() . Из теоремы Крамера следует, что обратные матрицы существуют только для невырожденных матриц и находятся единственным образом, какой бы способ не использовался для их вычисления. Количество арифметических операций при обращении матрицы порядка
. Из теоремы Крамера следует, что обратные матрицы существуют только для невырожденных матриц и находятся единственным образом, какой бы способ не использовался для их вычисления. Количество арифметических операций при обращении матрицы порядка ![]() по методу Гаусса равно числу
по методу Гаусса равно числу ![]() и является наименьшим по сравнению с другими точными методами. Для построения обратной матрицы
и является наименьшим по сравнению с другими точными методами. Для построения обратной матрицы ![]() для матрицы
для матрицы ![]() сначала составляют специальную расширенную матрицу
сначала составляют специальную расширенную матрицу ![]() . Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса. В результате матрица
. Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса. В результате матрица ![]() приводится к виду
приводится к виду ![]() . В преобразованной матрице
. В преобразованной матрице ![]() справа от единичной матрицы формируется именно обратная матрица
справа от единичной матрицы формируется именно обратная матрица ![]() . Действительно, матричное уравнение
. Действительно, матричное уравнение ![]() , составленное относительно неизвестных нам элементов матрицы
, составленное относительно неизвестных нам элементов матрицы ![]() , равносильно совокупности из
, равносильно совокупности из ![]() неоднородных систем уравнений:
неоднородных систем уравнений: ![]() . Правые части этих систем состоят из канонических арифметических вектор – столбцов
. Правые части этих систем состоят из канонических арифметических вектор – столбцов ![]() , а неизвестными являются столбцы
, а неизвестными являются столбцы ![]() искомой матрицы
искомой матрицы ![]() . Расширенная матрица этих
. Расширенная матрица этих ![]() неоднородных уравнений равна
неоднородных уравнений равна ![]() . Таким образом, когда расширенная матрица
. Таким образом, когда расширенная матрица ![]() приводится к виду
приводится к виду ![]() , происходит решение
, происходит решение ![]() неоднородных систем уравнений
неоднородных систем уравнений ![]() По методу Гаусса, а в преобразованной матрице
По методу Гаусса, а в преобразованной матрице ![]() справа от единичной матрицы формируется обратная матрица.
справа от единичной матрицы формируется обратная матрица.
Пример. Вычислим по методу Гаусса матрицу, обратную к .
.
Специальная расширенная матрица в нашем случае имеет вид:
![]() =
= .
.
Далее выполняются элементарные преобразования над расширенной матрицей по полной схеме метода Гаусса:
![]()
![]()

![]()
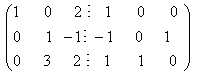
![]()
![]()
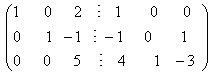
![]()
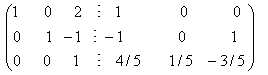
![]()
![]()
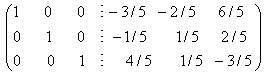 =
= ![]() .
.
Таким образом, в матрице ![]() справа от единичной матрицы сформирована обратная матрица
справа от единичной матрицы сформирована обратная матрица ![]() , в нашем случае равная
, в нашем случае равная
![]() =
= 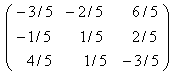 .
.
Правильность вычисления обратной матрицы всегда рекомендуется проверять непосредственно по ее определению ![]() , выбирая для контроля любое из равенств.
, выбирая для контроля любое из равенств.
| < Предыдущая | Следующая > |
|---|