5.5. Элементарные функции

Кроме функций, перечисленных в предыдущих параграфах, в школе изучают еще тригонометрические функции — синус, косинус, тангенс, котангенс, секанс и косеканс, причем последние четыре просто выражают­ся через синус и косинус:

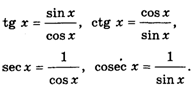
По определению, sin X = A, Cos х = B, где (A,B) — координаты точки М, которая лежит на окружности единич­ного радиуса с центром в начале координат, а Х — угол, образованный вектором ОМ и осью Х (см. рис. 21).

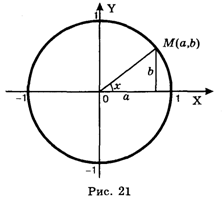
Если точка М сде­лает полный оборот и придет в исходное по­ложение, то угол Х Увеличится на 2p.* Но числа А и B в ре­зультате этой процеду­ры не изменятся. От­сюда вытекает, что синус, косинус и все другие тригонометри­ческие функции будут Периодическими функциями с периодом 2p, т. е. для них

Sin Х = sin (X + 2p) = sin (X + 4p) = ... = sin(X + 2pK),

Cos Х = cos (X + 2p) = cos (X + 4p) = ... = cos (X + 2pK),

Где K — любое целое число. Периодичность — важней­шее специфическое свойство тригонометрических функ­ций. Другие функции — степенная, показательная и логарифмическая — периодическими не являются. С по­мощью тригонометрических функций описываются са­мые разнообразные периодические процессы, происходящие в живой и неживой природе: колебательные и вращательные движения, волновые явления, движение планет, биологические ритмы и т. д.

* Угол здесь и дальше измеряется в радианах. Напоминаем, что полный угол равен 360° или 2P радиан.

Подумайте, является ли постоянная функция периодической.

Функции, как и числа, можно складывать, вычи­тать, умножать и делить. Например, если разделить од­ну линейную функцию на другую, то получим так называемую Дробно-линейную функцию:

Если сложить несколько степенных функций вида Axn, Где П — натуральное число или нуль, то получится Мно­гочлен. Например, многочлен второй степени

У = Ax2 + Bх + с

Получается как сумма трех функций:

У = ах2, У = Bх = Bх1, У = с = сх0.

Точно так же получается многочлен любой степени N:

У = а0 хN + A1 N–1 + A2 Xn–2 + ... + ап–1 х + аN.

Многочлены играют важную роль и математике и ее приложениях. Примерно 100 лет назад Карл Вейерштрасс* доказал, что любую непрерывную функцию можно приближать многочленами с любой степенью точности. В частности, приближенное значение функ­ции Eх находят по формуле

Чем больше N (число слагаемых), тем выше точность, т. е. тем меньше приближенное значение функции отли­чается от ее истинного значения.

* Карл Вейерштрасс (1815-1897) — выдающийся математик XIX в. В университете начал изучать юриспруденцию, но оста­вил ее, увлекшись математикой. Вейерштрасс одним из первых начал строго определять основные математические понятия.

Вычислим, например, с помощью многочленов значение массы кобальта (см. пример из предыдущего парагра­фа). Если ограничиться тремя слагаемыми, то получим:

.

Пользуясь этой формулой, находим:

M(5,2) = 100 • Е–0,676 » 100(1 – 0,676 + ½(–0,676)2) = 100 • 0,5525 = 55,25 Г.

Если же взять четыре слагаемых, то получим

ЕX » 1 + Х + х2 + х3.

Эта формула дает уже более точное значение:

M(5,2) » 100 = 50,10 Г.

Если один многочлен поделить на другой, получится Дробно-рациональная функция, например:

.

Кроме того, представляют интерес и более сложные вы­ражения:

У = х sin Х, Y = X + Sin X, y = (Ex + e–X)

И т. п.

Над функциями можно производить еще одну опе­рацию, которая не имеет аналога у чисел. Это операция Композиции. Рассмотрим, например, функции У = v2 и V = х – 1. Их композицией будет функция

Y = (X – 1)2,

Которая получается подстановкой значения V в выраже­ние для У. Точно так же функция

Представляет собой композицию функций У = ЕV и V = – х2.

Композиции двух или нескольких функций называются также Сложными функциями.

Теперь мы можем ответить на вопрос, что такое Эле­ментарная функция. Так называются постоянные, ли­нейные, степенные, показательные, логарифмические и тригонометрические функции, а также функции, кото­рые получаются из них с помощью конечного числа арифметических операций и операций композиции. На­пример, следующие функции являются элементарными:

У = ln cos Х, у = 2sin Х, у = lg Х + lg lg X.

Из определения ясно, что всякая элементарная функция может быть представлена в виде композиции наиболее простых элементарных функций, что дает возможность построить ее график. Именно так в школе исследуется многочлен второй степени (так называемый Квадрат­ный трехчлен).

Напомним, как это делается. Рассмотрим, например, многочлен

У = 2Х2 – 10Х + 12. (22)

Преобразуем правую часть, выделив полный квадрат:

2Х2 – 10Х + 12 = 2(Х2 – 5Х + 6,25) – 0,5 = 2(Х – 2,5)2 – 0,5.

В результате заданный многочлен можно записать следующим образом:

У = 2(Х – 2,5)2 – 0,5.

Теперь хорошо видно, что он представляет собой компо­зицию трех функций:

У = и – 0,5; U = 2V2; v = х – 2,5. (23)

Пользуясь этим, построим график многочлена (22). Сна­чала строим график известной нам функции U = 2V2 (см. рис. 22).

Рассмотрим далее первое из равенств (23):

Y = U – 0,5.

Оно означает, что у каждой точки М плоскости мы уменьшаем ее вторую координату U на 0,5, в результате чего получается новая вторая координата У. Эта операция равно­сильна тому, что мы поднимаем горизонтальную ось (ось V) на 0,5 вверх. В результате получаем картину, изображенную на рис. 23 (прежнее положение оси V обо­значено пунктиром).

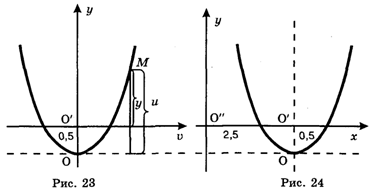
Далее рассмотрим третье ра­венство (23), которое запишем так:

Х = V + 2,5.

Оно означает, что к первой коор­динате V каждой точки плоскости мы прибавляем число 2,5 и получаем в результате новую первую координату Х. Это равносильно тому, что мы сдвигаем ось У на 2,5 единицы влево (см. рис. 24, на ко­тором прежнее положение оси Y обозначено пунктиром).

Итак, график многочлена второй степени (22) получается сдвигом параболы У = 2Х2 на 2,5 единицы вправо и 0,5 единицы вниз. Числа 2,5 и –0,5 являются коорди­натами вершины полученной таким образом параболы.

Ясно, что описанные построения можно проделать с любым многочленом второй степени, так что графиком любого многочлена второй степени является парабола.

Более того, с помощью аналогичных рассуждений можно строить графики и других элементарных функций.

УПРАЖНЕНИЯ

15. Постройте графики следующих функций:

А) У = 2Х–1 + 3; б) У = lg(X + 1); в) У = (Х – 1)3.

ТИПОВОЕ ЗАДАНИЕ

2. Процесс роста популяции описывается так называемой логистической функцией F(T) = . Здесь F(T) — размер популяции в момент времени T. По­стройте график этой функции.

< Предыдущая		Следующая >