5.3. Степенные функции
Функция
Y = Х2 (15)
Называется Квадратичной, а ее график называется Параболой (см. рис. 14).

Точка О называется Вершиной параболы. Ось Y является Осью симметрии параболы, т. к. для каждой точки М(х, у), лежащей на параболе, симметричная ей относительно оси Y точка М'(–х, у) также лежит на параболе. Другими словами, если чертеж перегнуть по оси Y, то левая половина параболы совпадет с правой.
Переменная Х, стоящая в правой части уравнения (15), может принимать любые значения. Если Х возрастает от –¥ до нуля (Х Î [–¥,0]), то У = Х2 убывает от +¥ до нуля. Следовательно, на промежутке (–¥,0) функция (15) убывает. Это хорошо видно на рисунке: левая часть графика идет сверху вниз, если двигаться в направлении возрастания координаты Х, т. е. слева направо. Правая часть графика демонстрирует нам тот факт, что функция возрастает на промежутке [0,+ ¥).
Найдем теперь график обратной функции, для чего, как и в случае с линейной функцией, поменяем местами переменные Х И у А затем выразим У. После замены получим Х = у2, откуда У = ![]() или У = –
или У = –![]() . Таким образом, мы получили две функции. Первая (У =
. Таким образом, мы получили две функции. Первая (У = ![]() ) будет обратной для функции Х = У2, х ³ 0, графиком которой является правая ветвь параболы; функция У = –
) будет обратной для функции Х = У2, х ³ 0, графиком которой является правая ветвь параболы; функция У = –![]() является обратной для функции Х = у2, х £ 0, графиком которой является левая половина параболы (см. рис. 15).
является обратной для функции Х = у2, х £ 0, графиком которой является левая половина параболы (см. рис. 15).

УПРАЖНЕНИЯ
10. Постройте графики следующих функций и функций, им обратных:
А) У =2Х2; б) У = –Х2; в) У = –2Х2.
Степенная функция
Y = X3 (16)
Называется Кубической. Ее график (см. рис. 16) называется Кубической параболой.
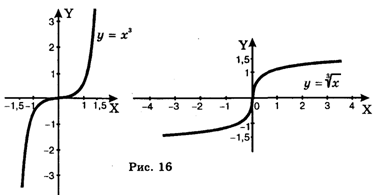
Обратной к функции (16) будет Х = У3 или У = ![]() . Ее график (см. рис. 16) также будет кубической параболой. Обе параболы симметричны относительно начала координат. Действительно, если уравнению (16) удовлетворяют координаты точки М(Х, у), то ему же удовлетворяют и координаты точки М'(–х –у), которая симметрична М относительно начала координат.
. Ее график (см. рис. 16) также будет кубической параболой. Обе параболы симметричны относительно начала координат. Действительно, если уравнению (16) удовлетворяют координаты точки М(Х, у), то ему же удовлетворяют и координаты точки М'(–х –у), которая симметрична М относительно начала координат.
На рис. 17 приведены графики степенной функции У = Х4 и соответствующих обратных функций.

УПРАЖНЕНИЯ
11. Постройте графики заданных функций и функций, им обратных:
![]()
| < Предыдущая | Следующая > |
|---|