3.1. Элементы комбинаторики. Комбинаторные задачи и методы их решения
В практической деятельности юристу часто приходится иметь дело с самыми разнообразными ситуациями. Умение анализировать сложившуюся обстановку, адекватно ее оценивать и делать правильные выводы является важным качеством каждого профессионала. Во многих случаях практика приводит к так называемым Комбинаторным задачам.
Комбинаторные задачи связаны: а) с выбором из некоторой группы предметов тех, которые обладают заданными свойствами; б) с расположением этих предметов в определенном порядке; в) с расчетом числа возможных комбинаций. Ниже мы приводим примеры таких задач и обсуждаем способы их решения.
Задача 1. 90 дней майора Зимина
Майор Зимин ежедневно формирует наряд для поддержания общественного порядка в центре города Дрюкова. Наряд состоит из двух человек — старшего наряда и дежурного. В распоряжении майора находится 10 милиционеров. Чтобы избежать длительных контактов милиционеров с нарушителями правопорядка, майор составляет наряд каждый день по-разному. Сколько дней майор Зимин может спать спокойно (т. е. до тех пор, пока какой-нибудь наряд не повторится)?
Решение. Прежде всего, майор занумеровал личный состав числами 1, 2, ... , 10. Далее, поскольку майор был страстным болельщиком, он составил таблицу наподобие той, в которой отмечал результаты футбольного первенства:
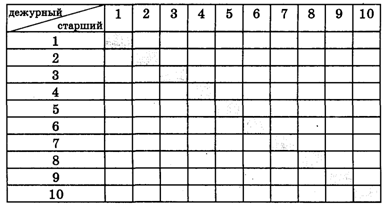
В клетках он проставил даты дежурств. Каждая клетка находится на пересечении некоторого столбца и некоторой строки, номера которых и определяют состав соответствующего наряда.
При этом пары вида (1,7) и (7,1) считаются разными, т. к. хотя в них люди одни и те же, но должности у них разные. Клетки (1,1), (2,2), ... , (10,10) заштрихованы потому, что один и тот же человек не может быть и старшим и дежурным одновременно.
Будучи от природы человеком весьма сообразительным, майор Зимин заметил, что в каждом из десяти столбцов записано 9 вариантов наряда, поэтому 9 • 10 = 90 дней он может спать спокойно.
Задача 2. Когда следствие ведут знатоки
В Стукове происходят два ЧП в день. На место происшествия отправляют оперативную группу из трех человек: следователя, оперативника и эксперта. В УВД несут службу 3 следователя, 2 оперативника и 3 эксперта. График их работы составляется таким образом, чтобы каждая очередная опергруппа отличалась от всех предыдущих (пока это будет возможно). Трое друзей — следователь Зубов, оперативник Прокопенко и эксперт Зульфия всегда добиваются успеха. Как часто эта группа попадает в график?
Решение. Будем перебирать всевозможные составы оперативной группы, учитывая, что следователя можно выбрать тремя способами (С1, C2, С3), оперативника — двумя (O1 и O2), а эксперта — тремя способами (Э1, Э2, Э3).
Составим так называемое Дерево. Проведем из некоторой точки А три отрезка: АС1, АС2 и АС3, каждый из которых символизирует выбор следователя (рис. 5).
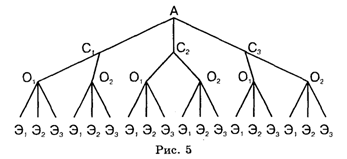
Из концов этих отрезков проведем по два новых отрезка С1О1, С1О2, C2O1, ... , С3О2, каждый из которых показывает, кто из оперативников включен в опергруппу.
Из концов последних отрезков проведем еще три отрезка с концами Э1, Э2, Э3, которые указывают на назначение в группу одного из трех экспертов. Изображенную на рисунке схему и называют деревом. Всякий путь вдоль ветвей этого дерева от его вершины А к какой-либо вершине Э1, Э2 или Э3 изображает состав одной из оперативных групп. Например, путь АС2О1Э3 Изображает оперативную группу, в которую включены следователь C2, оперативник О1 и эксперт Э3.
Чтобы найти число всех путей, перемножим число всех отрезков, выходящих из точки А, на число отрезков с началом в точках С1, C2, С3 и на количество отрезков, проведенных из точек О1 и O2. Полученное произведение 3 • 2 • 3 = 18 дает число всевозможных различных оперативных групп. Так как в день выезжают две группы, то через 18 : 2 = 9 дней группы начнут повторяться. Итак, знатоки (Зубов, Прокопенко и Зульфия) встречаются на выездах раз в 9 дней.
Задача 3. Случай с адвокатом
У адвоката N из юридической фирмы «Брюковские адвокаты» произошла досадная неприятность с компьютером — сразу после включения оперативная система зависла и на экране монитора появилось сообщение:
«Привет! Я — компьютерный вирус «Загадка Сфинкса». Ты должен ответить на 12 вопросов, которые записаны с помощью дренеегипетских иероглифов. На каждый вопрос можно ответить только «да» или «нет». Если через 10 дней ты не сможешь правильно ответить на мои вопросы или попытаешься выключить компьютер — твой винчестер умрет».
В компьютере содержалась очень важная информация, восстановить, которую, в случае потери, было бы практически невозможно. Но адвокат N не поддался панике, а придумал два способа решения проблемы. Во-первых можно попробовать расшифровать иероглифы с помощью специального словаря. Адвокат выяснил, что такой словарь есть в брюковской библиотеке, но получить его можно будет только через 8 дней. Поэтому он решил действовать вторым способом: перебирать все возможные комбинации ответов «да» и «нет» на 12 непонятных вопросов, пока не обнаружится правильный вариант. Чтобы не сбиться, адвокат решил записывать каждую комбинацию ответов в виде следующей таблички:
![]()
На составление очередной комбинации ответов и ввод ее в компьютер адвокат тратит одну минуту. Успел ли он сделать работу вовремя и спасти винчестер, если работал по 6 ч в сутки, а правильная комбинация оказалась последней?
Решение. Число комбинаций так велико, что составление таблицы (как в задаче 1) или графической схемы (как в задаче 2) было бы слишком трудоемким. Поэтому мы ограничимся только логическими рассуждениями.
Если бы вопрос был один, то на него было бы всего два варианта ответов: «да» и «нет». Если бы вопросов было два, то комбинаций ответов было бы 4: да-да, нет-нет, да-нет, нет-да. Если бы вопросов было три, то число комбинаций ответов было бы 8, т. к. к каждому из предыдущих четырех пришлось добавить либо «да», либо «нет» при ответе на третий вопрос. Таким образом, при добавлении одного вопроса число комбинаций ответов удваивается: четыре вопроса дают 8 • 2 = 16 комбинаций ответов, на пять вопросов получается 24 • 2 = 25 комбинаций и т. д., двенадцать вопросов дадут 212 = 4096 комбинаций.
Итак последняя — нужная — комбинация ответов появится через 4096 мин работы. Разделив на 60, мы получим 68 ч 16 мин, что при шестичасовом рабочем дне составляет более одиннадцати суток.
Мы обсудили три задачи, в каждой из которых занимались расчетом числа определенных комбинаций. На самом деле, все эти задачи решаются по одной и той же логической схеме. Сейчас мы запишем общие формулы для решения любых задач подобного типа.
В наиболее общем виде решение первой задачи выглядит так.
Пусть требуется выполнить последовательно два действия (например, первое действие — выбор старшего наряда, второе — выбор дежурного). Если первое действие выполняется т различными способами, а второе — п различными способами, то оба действия можно выполнить т • п различными способами. Это утверждение называется Правилом умножения.
Задача 2 обобщается следующим образом: Пусть требуется последовательно выполнить три действия, причем, первое действие может быть выполнено M способами, второе — N способами и третье — K способами. Тогда три действия можно выполнить т • п • k способами.
Попробуйте сформулировать в общем виде аналогичную задачу для произвольного числа действий. Например, во второй задаче всего 12 действий и каждое из них выполняется двумя способами («да» и «нет»). Поэтому ответ будет 2 • 2 • 2 • ... • 2 — всего 12 сомножителей, т. е. 212 = 4096.
Таблица и дерево, с помощью которых мы решали первые две задачи, описывают правило умножения в некоторой специфической форме.
Правило умножения — хотя и простой, но важный математический факт. Поэтому его необходимо строго доказать. Это будет сделано в следующем параграфе.
УПРАЖНЕНИЯ
1. В забеге участвовало 5 спортсменов. Сколькими способами можно предсказать распределение первых трех мест, если известно, что эти спортсмены всегда показывают разные результаты?
2. Замок сейфа открывается, если набрана правильная комбинация из четырех цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число безуспешных попыток.
3. Некто написал 6 новогодних поздравлений своим друзьям, затем взял 6 разных конвертов и разложил открытки по конвертам наудачу. Каково число всех возможных комбинаций?
| < Предыдущая | Следующая > |
|---|