2.3. Интервальный ряд. Гистограмма

При обработке большого числа экспериментальных данных их предварительно группируют и оформляют в виде так называемого Интервального ряда.

Пример 1. Средняя месячная зарплата за год каждо­го из пятидесяти случайно отобранных работников хо­зяйства такова:

317 304 230 285 290 320 262 274 205 180 234 221 241 270 257 290 258 296 301 150 160 210 235 308 240 370 180 244 365 130 170 250 370 267 288 231 253 315 201 256 279 285 226 367 247 252 320 160 215 350.

Здесь переменной величиной X является средняя месячная зарплата. Как видно из приведенных данных, наименьшее значение величины Х равно 130, а наи­большее — 370. Таким образом, диапазон наблюдений представляет собой интервал 130 – 370, длина которого равна 370 – 130 = 240.

Разобьем диапазон наблюдений на части (разряды) Так, чтобы каждый разряд содержал несколько экспе­риментальных данных. Например, разделим интервал 130 – 370 на 6 равных частей, тогда длина каждого раз­ряда будет 40. Границами разрядов будут числа 130, 170, 210, 250, 290, 330, 370 (рис. 3).

Подсчитаем число значений, попавших в каждый разряд. Например, в первый разряд попадают следующие числа: 150 (1 раз), 160 (2 раза), 130 (1 раз), 170 (1 раз). Поскольку число 170 находится на границе между пер­вым и вторым разрядами, мы включим его и в первый и во второй разряды, но с кратностью 1/2. Сложив кратно­сти, мы получим Абсолютную частоту первого разряда:

M1 = 1 + 2 + 1 + 0,5 = 4,5.

Разделив абсолютную частоту на число П всех наблюде­ний, получим Относительную частоту Попадания величины Х в первый разряд:

Проделав вычисления для всех разрядов, мы полу­чим следующую таблицу.

Таблица 6

Здесь Mi — абсолютные частоты, — относитель­ные частоты. Табл. 6 называется Интервальным рядом.

Сумма всех абсолютных частот равна числу всех приведенных в табл. 6 значений переменной величины:

4,5 + 5 + 12 + 14,5 + 9 + 5 = 50.

Это свойство используется для проверки правильности вычислений. Из него следует, что сумма всех относи­тельных частот равна единице:

0,09 + 0,10 + 0,24 + 0,29 + 0,18 + 0,10 = 1.

Интервальный ряд изображают графически в виде Гистограммы, которая строится так. Сначала вычисляют плотности частот H1, H2, H3, ... , разделив относительную частоту каждого разряда на его длину:

Затем выбирают на плоскости систему координат и откладывают на оси Х значения 40, 80, 120, ... , соответ­ствующие границам разрядов. На каждом из отрезков длины 40, как на основании, строят прямоугольник, высота которого равна плотности частоты соответствую щего разряда. Полученная фигура и называется Гисто­граммой. Она изображена на рис. 4.

Заметьте, что высоты H1, H2, ... , H6 прямоугольников, образующих гистограмму, выбраны так, что их площади будут , т. е. равны соответствующим отно­сительным частотам. Отсюда вытекает такое правило:

Для того, чтобы найти долю тех значений величи­ны. X, которые попадают в некоторый интервал, нужно найти площадь той части гистограммы, основанием которой является данный интервал.

Определим, например, долю значений величины X, Принадлежащих интервалу 210 – 300. Для этого вычислим площадь фигуры с основанием 210 – 300 (на рисунке она выделена штриховкой). Площади первых двух прямоуголь­ников, составляющих фигуру, равны соответственно = 0,24 и = 0,29; площадь третьего равна 10 • 0,0045 = 0,045. Сумма площадей 0,24 + 0,29 + 0,045 = 0,575 и дает нужное число. Иными словами, 57,5% значений величины Х находится в границах от 210 до 300.

Как мы заметили в начале параграфа, интервальный ряд составляют при обработке больших массивов ин­формации. В таких случаях, как правило, отдельные значения величины Х не фиксируются, а подсчитывает­ся количество ее значений, попавших в каждый разряд (т. е. абсолютные частоты). Поэтому исследователь не знает отдельных значений наблюдаемой величины Х и не может воспользоваться формулами (1), (5) и (7) для вычисления среднего арифметического, дисперсии и среднего квадратического отклонения. Но приближен­ное значение этих числовых характеристик можно най­ти с помощью интервального ряда. Для этого сначала находят середины разрядов: (здесь K — Число всех разрядов интервального ряда); затем прово­дят вычисления по следующим формулам:

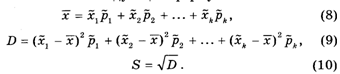
Результаты расчетов по данным табл. 6 сведены в сле­дующую таблицу:

Таблица 7

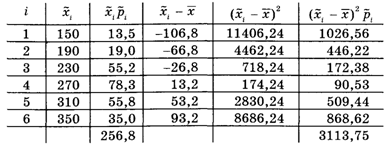
В первом столбце записаны номера разрядов, во вто­ром — числа (середины разрядов), в третьем — произведения , и т. д. Таблица заполняется по столбцам. Середину разряда вычисляем как полусумму его границ:

Согласно формуле (8), сумма чисел третьего столбца да­ет среднее арифметическое = 256,8. Оно записано в последней строке этого столбца. Сумма чисел последнего столбца равна дисперсии D = 3113,75 [см. формулу (9)]. Наконец, по формуле (10) определяем среднее квадратическое отклонение S = = 55,80.

Интервальный ряд, гистограмма и числовые характеристики, найденные по формулам (8)—(10), составляют Математическую модель средней заработной платы. Она используется при проведении различных социологи­ческих исследований, например, при определении уров­ня жизни работников какой-либо отрасли.

ТИПОВЫЕ ЗАДАНИЯ

1. Для проведения демографических исследований выбрали 50 семей и получили следующие данные о ко­личестве членов семьи:

2 5 3 4 1 3 6 2 4 3 4 1 3 5 2 3 4 4 3 3 2 5 3 4 4

3 3 4 4 3 2 5 3 1 4 3 4 2 6 3 2 3 1 6 4 3 3 2 1 7.

Укажите переменную величину; составьте табл. 5; найдите числовые характеристики — среднее арифмети­ческое, дисперсию, среднее квадратическое отклонение.

2. Управление сельского хозяйства Дрюковского района представило сводку по пятидесяти хозяйствам. Согласно этой сводке, урожайность ржи в них составила (в центнерах с гектара):

17.5 17.8 18.6 18.3 19.1 19.9 20.6 20.1 22 21.4 17.5 18.5 19 20 22 20.6 19.1 18.6 17.9 19.1 22 19 17.5 22 22.6 21 21.4 19 17.8 18.3 19.9 20.1 21.4 18.5 20 20.6 18.6 21.4 21 20 20 18 18 18 17.5 18.6 19.1 20.6 17.5 18.6 .

Постройте интервальный ряд (табл. 6), гистограмму, составьте табл. 7 и по формулам (8)-(10) найдите число­вые характеристики — среднее арифметическое, диспер­сию, среднее квадратическое отклонение.

< Предыдущая		Следующая >