137. Понятие первообразной и неопределенного интеграла
Основная задача Дифференциального исчисления – это нахождение производной 
по данной функции 
.
В науке и технике многие задачи требуют решения обратных проблем, когда по данной производной 
нужно найти функцию 
.
Функция называется Первообразной для функции 
на интервале 
, если в любой точке этого интервала функция дифференцируема и .
Например, функция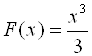 
– это первообразная для функции 
на всей числовой прямой 
, так как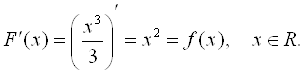 
Очевидно, что 
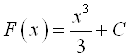, также является первообразной для функции 
, где 
– постоянная.
Теорема. Функция, непрерывная на интервале , имеет множество первообразных на этом интервале, которые отличаются на постоянную величину.
Нахождение первообразной по данной функции является Основной задачей Интегрального исчисления.
Множество всех первообразных 
для данной функции на интервале называется Неопределенным интегралом от функции на этом интервале и обозначается символом 
.
Читают так: "Интеграл эф от икс де-икс".
Если F(X) – любая первообразная функции , то
,
Где 
– подынтегральная функция; 
– подынтегральное выражение; 
– переменная интегрирования; 
– знак неопределенного интеграла; – произвольная постоянная.
Например,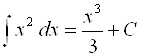 
.
Нахождение неопределенного интеграла (или первообразной) от данной функции называется Интегрированием этой функции.
Интегрирование есть действие, обратное дифференцированию.
|
Ответьте на вопросы |
1. Какая функция называется первообразной функции в интервале 
?
2. Сколько первообразных имеет функция, непрерывная в интервале ?
3. Сформулируйте основную задачу интегрального исчисления.
4. Что такое неопределенный интеграл?
5. Прочитайте выражение 
и назовите составляющие его символы: 
; 
; ; .
6. Как называется действие нахождения первообразной?
| < Предыдущая | Следующая > |
|---|
