054. Способы задания функций
Функция задана, если известны множества ![]() ,
, ![]() и закон соответствия.
и закон соответствия.
Существуют три основных способа задания функции: аналитический, табличный и графический.
1. Аналитический способ состоит в том, что функцию задают формулой, например ![]() ,
, ![]()
![]() .
.
2. Табличный способ состоит в том, что соответствие между аргументом и функцией задают в виде таблиц.
Например, существуют таблицы кубов чисел, квадратов чисел, тригонометрических функций, логарифмов и так далее.
3. Графический способ состоит в том, что график функции ![]() изображают в системе координат
изображают в системе координат ![]() .
.
Чтобы построить систему координат ![]() , возьмем на плоскости две взаимно-перпендикулярные координатные оси. Эти оси пересекаются в точке
, возьмем на плоскости две взаимно-перпендикулярные координатные оси. Эти оси пересекаются в точке ![]() (рис. 5.2.).
(рис. 5.2.).
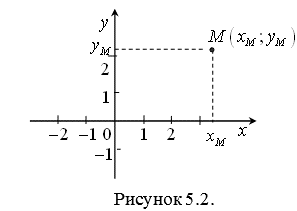
Прямая ![]() называется осью абсцисс, а прямая
называется осью абсцисс, а прямая ![]() – осью ординат. Точка
– осью ординат. Точка ![]() – это начало координат. На каждой оси выбирается положительное направление и единица измерения (масштаб).
– это начало координат. На каждой оси выбирается положительное направление и единица измерения (масштаб).
Каждая точка ![]() на координатной плоскости имеет две координаты: абсциссу
на координатной плоскости имеет две координаты: абсциссу ![]() и ординату
и ординату ![]() .
.
График функции ![]() – это множество точек плоскости с координатами
– это множество точек плоскости с координатами ![]() и
и ![]() (рис. 5.3).
(рис. 5.3).

Если ![]() и функция
и функция ![]() определена при
определена при ![]() , то значение функции записывают так:
, то значение функции записывают так:
![]() или
или ![]() , или
, или ![]() .
.
Когда функция задана аналитически, считают, что она определена для тех значений аргумента, для которых математические операции в формуле выполнимы, то есть аналитическое выражение имеет смысл. Множество всех таких значений называют естественной областью определения функции и обозначают ![]() . Естественная область определения не всегда соответствует реальным (физическим) значениям аргумента.
. Естественная область определения не всегда соответствует реальным (физическим) значениям аргумента.
Например, для функции ![]() естественной областью определения будет
естественной областью определения будет ![]() , но если
, но если ![]() – площадь круга радиуса
– площадь круга радиуса ![]() , то
, то ![]() может быть только положительным.
может быть только положительным.
Для нахождения ![]() надо учитывать следующие четыре основных ограничения.
надо учитывать следующие четыре основных ограничения.
1. Если ![]() , то
, то ![]() . 3. Если
. 3. Если ![]() то
то ![]() .
.
2. Если 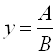 , то
, то ![]() . 4. Если
. 4. Если  , то
, то ![]() .
.
Если аналитическое выражение функции содержит несколько таких выражений, область ее определения будет пересечением областей для отдельных ограничений.
Например, для функции 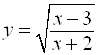 область определения
область определения ![]() выражается условием
выражается условием ![]() . Это значит
. Это значит ![]() или
или ![]() .
.
| < Предыдущая | Следующая > |
|---|