023. Алгебраические выражения

Алгебраическое выражение – это выражение, которое состоит из чисел, переменных и математических знаков. Выражение может содержать скобки, рациональную степень переменной (с целым или дробным показателем), знак модуля.

Например, алгебраические выражения – это: .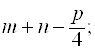

Область допустимых значений (ОДЗ) алгебраического выражения – это такие значения переменных, при которых это выражение имеет смысл.

Пример 3. Найдите ОДЗ алгебраического выражения: .

Решение. Если , то выражение не имеет смысла.

Ответ. ОДЗ: .

Пример 4. Найдите ОДЗ выражения: .

Решение. Из условия имеем:. Это значит, что если или , то выражение не имеет смысла.

Ответ. ОДЗ: .

Рассмотрим рисунок 3.1 подробнее, для этого дадим характеристику каждому компоненту рисунка.

Алгебраические выражения могут быть рациональными и иррациональными.

Рациональное выражение – это выражение, в котором содержатся действия сложения, вычитания, умножения, деления, возведения в степень (здесь показатель степени – это натуральное число).

Например, ; ; – это рациональные выражения.

Рациональные выражения могут быть Целыми и Дробными.

Целое рациональное выражение не содержит деления на буквенное выражение. Например, ; – это целые рациональные выражения.

Целые рациональные выражения подразделяются на одночлены и многочлены.

Одночлен – это произведение числового коэффициента на натуральную степень переменных.

Например, ; ; 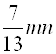– это одночлены, где ; ; – это числовые коэффициенты; ; ; – это буквенные выражения.

Степень одночлена – это сумма показателей степеней всех переменных одночлена.

Например, одночлен – это одночлен шестой степени одночлен – это одночлен четвертой степени 7 – это одночлен нулевой степени.

Одночлен имеет Стандартный вид, если числовой коэффициент стоит на первом месте (перед буквенным выражением), а неизвестные множители записаны в алфавитном порядке.

Одночлены называются Подобными, если они имеют одинаковые буквенные выражения.

Привести подобные одночлены (члены) – это значит найти их сумму или разность.

Например, ; ; – это подобные одночлены.

Пример 5. Приведите подобные члены: .

Решение. ; ; .

Ответ. .

Многочлен – это алгебраическая сумма одночленов (их сумма или разность).

Например, – это многочлен.

Степень многочлена – это степень его старшего члена.

Например, многочлен – это многочлен четвертой степени; многочлен – это многочлен пятой степени.

Дробное рациональное выражение содержит деление на выражение с переменными. Дробное рациональное выражение называют алгебраической дробью.

Например, 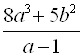; 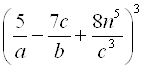– это алгебраические дроби.

Используют и другое определение алгебраической дроби.

Выражение вида , где и – это многочлены или одночлены, называется Алгебраической дробью.

Область допустимых значений (ОДЗ) Алгебраической дроби это множество значений переменной, при которых ее знаменатель не равен нулю ().

Алгебраическая дробь равна нулю, если ее числитель равен нулю, т. е. .

Если в алгебраическом выражении используется возведение переменных в дробную степень (извлечение корня из переменных), то такое алгебраическое выражение называется Иррациональным.

Например, ; – это иррациональные выражения.

Алгебраические выражения могут быть рациональными и иррациональными.

Рациональные выражения разделяются на целые и дробные.

Целые рациональные выражения состоят из одночленов и многочленов.

Дробные рациональные выражения включают в себя алгебраические дроби.

< Предыдущая		Следующая >