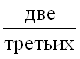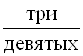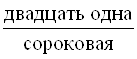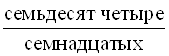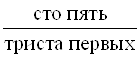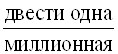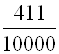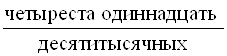010. Обыкновенные дроби

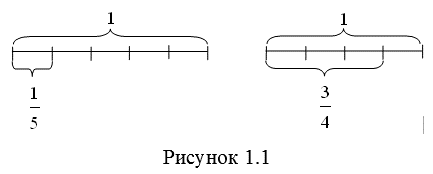
Обыкновенная дробь – это одна или несколько равных частей единицы. Например, дробь означает, что единица разделена на 5 равных частей и взята одна такая часть. Дробь означает, что единица разделена на 4 равные части и взяты три такие части (рис. 1.1).

– это обыкновенная дробь, ; ; ; – это тоже обыкновенные дроби.

Таблица 1.11 – Числительные

	Сколько?	Какой? (по порядку)	Какая?	Каких?
1	Один	Первый	Первая	Первых
2	Два	Второй	Вторая	Вторых
3	Три	Третий	Третья	Третьих
4	Четыре	Четвертый	Четвертая	Четвертых
5	Пять	Пятый	Пятая	Пятых
6	Шесть	Шестой	Шестая	Шестых
7	Семь	Седьмой	Седьмая	Седьмых
8	Восемь	Восьмой	Восьмая	Восьмых
9	Девять	Девятый	Девятая	Девятых
10	Десять	Десятый	Десятая	Десятых
...
20	Двадцать	Двадцатый	Двадцатая	Двадцатых
...
100	Сто	Сотый	Сотая	Сотых
...
200	Двести	Двухсотый	Двухсотая	Двухсотых
...
500	Пятьсот	Пятисотый	Пятисотая	Пятисотых
...

– это Обыкновенная дробь, "" – Числитель дроби, "" – это Знаменатель дроби.

Таблица 1.12 – Обыкновенные дроби

Пример		Пример

Если числитель дроби меньше чем знаменатель, то это Правильная дробь. Если числитель дроби больше или равен знаменателю, то это Неправильная дробь.

Если дробь неправильная, то ее можно записать как Смешанное число.

Например, ; ; – это правильные дроби; ; ; – это неправильные дроби; ; ; ; 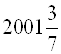– это смешанные числа.

Смешанное число – это сумма целой и дробной части.

Например: .

Чтобы записать неправильную дробь как смешанное число, нужно числитель дроби разделить на знаменатель.

Смешанные числа читаем так:

– одна целАя, три седьмых;

– три целЫх, одна пятая;

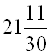– двадцать одна целАя, одиннадцать тридцатых;

– пятьдесят четыре целЫх, две двадцать первых.

Пример 10. Запишите неправильную дробь как смешанное число.

Ответ.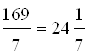

Пример 11. Запишите смешанное число как неправильную дробь.

Решение. .

Ответ. .

Основное свойство дроби. Величина дроби не изменится, если числитель и знаменатель дроби умножить или разделить на одинаковое число, не равное нулю.

Например, ; .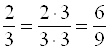

Сократить дробь – это значит, что числитель и знаменатель дроби нужно разделить на одинаковое число, не равное нулю.

Например, – мы сократили дробь на "2";

– мы сократили дробь на "8".

Для того чтобы выполнять арифметические действия с обыкновенными дробями, нужно уметь приводить эти дроби к общему знаменателю.

Пример 12. Приведите дроби и к общему знаменателю.

Решение. Дроби и имеют разные знаменатели: 7 и 5. Используем основное свойство дроби и заменим эти дроби другими дробями. Для этого умножим числитель и знаменатель дроби на дополнительный множитель 5, получим: ; умножим числитель и знаменатель дроби на дополнительный множитель 7, получим: .

Ответ. ; .

Такое преобразование называется приведением дробей к общему знаменателю.

Пример 12 можно решить иначе. Например, дроби и можно привести к общему знаменателю 70: ; ,

Или к общему знаменателю 105: ; ,

Или к любому другому знаменателю, который делится одновременно и на 7 и на 5.

Таким образом, привести дроби к общему знаменателю можно многими способами. Но обычно удобно приводить дроби к Наименьшему общему знаменателю (НОЗ).

НОЗ дробей равен наименьшему общему кратному (НОК) знаменателей данных дробей.

Чтобы привести дроби к НОЗ, нужно:

1) найти НОК знаменателей дробей;

2) вычислить дополнительные множители (для этого нужно разделить НОК на каждый знаменатель);

3) умножить числитель и знаменатель каждой дроби на дополнительные множители.

Пример 13. Приведите к наименьшему общему знаменателю дроби и .

Решение. Найдем наименьшее общее кратное чисел 24 и 30:

.

, поэтому, чтобы привести дробь к знаменателю 120, нужно ее числитель и знаменатель умножить на дополнительный множитель 5: .

, поэтому, чтобы привести дробь к знаменателю 120, нужно ее числитель и знаменатель умножить на дополнительный множитель 4: .

Ответ. Мы привели дроби к НОЗ: ; .

Таблица 1.13 – Действия с обыкновенными дробями и смешанными числами

Действие	Правило	Пример
Сложение дробей	Чтобы сложить дроби, нужно привести дроби к наименьшему общему знаменателю (НОЗ) и числители сложить.	, 6 – это НОЗ.
Вычитание дробей	Чтобы вычесть дроби, нужно привести дроби к наименьшему общему знаменателю (НОЗ) и числители вычесть.	, 14 – это НОЗ.
Умножение дробей	Чтобы умножить дроби, нужно умножить числители и полученный результат записать в числитель; умножить знаменатели и полученный результат записать в знаменатель. Если можно, то сократить дробь.	.
Деление дробей	Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй дроби. ( и – это обратные дроби.)	.
Сравнение дробей	Чтобы сравнить дроби, нужно привести их к НОЗ и сравнить их числители.	и . Приведем дроби к НОЗ: и , , поэтому .
Сложение, вычитание, умножение и деление смешанных чисел	Чтобы выполнить действия (сложение, вычитание, умножение, деление) со смешанными числами, удобно записать их как неправильные дроби, а потом выполнить действия.	1) 2)

< Предыдущая		Следующая >