06. Комбинаторные задачи и методы их решения
Задачи комбинаторики следующие:
- выбор из некоторой группы предметов тех, которые обладают некоторыми свойствами;
- расположение этих предметов в определенном порядке;
- расчет числа возможных комбинаций.
Рассмотрим несколько примеров.
Пример 1. Имеется 10 милиционеров. Из них назначается ежедневный наряд из двух человек: старшего наряда и дежурного. Чтобы избежать длительных контактов с нарушителями, каждый день назначается новый наряд. Сколько дней наряды не будут повторяться?
Решение. Составим таблицу:
|
Дежурный |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 | ||||||||||
|
2 | ||||||||||
|
3 | ||||||||||
|
4 | ||||||||||
|
5 | ||||||||||
|
6 | ||||||||||
|
7 | ||||||||||
|
8 | ||||||||||
|
9 | ||||||||||
|
10 |
Клетки по диагонали таблицы (1,1), (2,2),…, (10,10) исключаются. Остаются по 9 клеток в каждой строке, всего 90 клеток, каждая из которых соответствует своему составу наряда.
Пример 2. В районе в среднем случается 2 ЧП в день. Опергруппа обычно состоит из трех человек: следователя, оперативника и эксперта. В УВД служат 3 следователя, 2 оперативника и 3 эксперта. Каждая группа, пока это возможно, отличается от предыдущих. Через какое время группы начнут повторяться?
Решение. Произведем перебор составов опергруппы. Обозначим следователей С1, С2 и С3, оперативников О1 и О2 и экспертов Э1, Э2 и Э3. Составим дерево различных комбинаций.
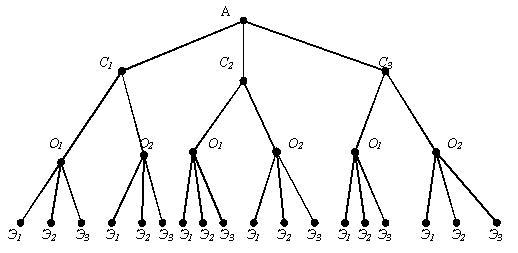
Число всех путей (каждый путь – состав опергруппы) равно 3×2×3 = 18. В день происходит 2 происшествия, т. е. через 18:2 = 9 дней группы начнут повторяться.
Пример 3. Случай с адвокатом. Компьютерный вирус на компьютере адвоката предлагает ему последовательно ответить на 12 вопросов «да» или «нет» и даёт срок 10 дней. Адвокат решил перебрать все возможные комбинации ответов. Каждый вариант требует ввода и занимает по времени 1 минуту. Успеет ли адвокат ответить правильно, если он тратит на это ежедневно по 6 часов?
Решение. Одна комбинация даёт два варианта ответа, две комбинации – уже 4 варианта и т. д. Здесь 4096 вариантов, т. е. 212. На все ответы требуется 4096 минут. Разделим на 60, получим 68 часов 16 минут, что при 6 – часовом рабочем дне составляет более 11 суток. Значит, адвокат не успеет!
Сформулируем правило умножения. Пусть требуется выполнить последовательно 2 действия. Если первое действие выполняется M различными способами, а второе – N различными способами, то оба действия можно выполнить M×N различными способами.
Это правило обобщается на произвольное число последовательных действий.
| < Предыдущая | Следующая > |
|---|
 Старший
Старший