05. Интервальный ряд и гистограмма

При обработке большого числа экспериментальных данных их предварительно группируют и оформляют в виде так называемого интервального ряда.

Пример. Рассмотрим среднюю месячную зарплату 50 случайно отобранных работников предприятия:

317	304	230	285	290	320	262	274	205	180	234	221	241
270	257	290	258	296	301	150	160	210	235	308	240	370
180	244	365	130	170	250	370	267	288	231	253	315	201
256	279	285	226	367	247	252	320	160	215	350

Величина Х здесь – средняя месячная зарплата. Наименьшее её значение – 130, наибольшее – 370. Диапазон составляет 130¸270, его длина 370 – 230 = 240.

Разобьем диапазон на части (разряды) так, чтобы каждый разряд содержал несколько экспериментальных данных. Например, на 6 равных частей: 240 : 6 = 40 – длина одного разряда. Границы: 130, 170, 210, 250, 290, 330, 270.

Подсчитаем число значений в каждом разряде, например, разряд 130¸170: 130, 170, 150,160,160; поскольку значение 170 попадает на границу 1 – го и 2 – го разрядов, включим его и в 1 – й, и во 2 – й разряды, но с с кратностью ½. Сложим кратности, получим абсолютную частоту 1 – го разряда:

M1 = 1 + ½ + 1+2 = 4 ½ .

Относительная частота попадания Х в 1 – й разряд равна:

И т. д. Результаты можем свести в таблицу:

Таблица 6

	130 - 170	170 - 210	210 - 250	250 - 290	290 - 330	330 – 370
	4,5	5	12	14,5	9	5
	0,09	0,1	0,24	0,29	0,18	0,1

Таблица 6 называется интервальным рядом. Для проверки правильности вычислений используется свойство:

,

А также свойство

.

Графически интервальный ряд изображается в виде гистограммы, которая строится так. Сначала вычисляют плотности частот делением относительной частоты каждого разряда на его длину:

, где DХ = 40;

; ; ; ;

.

Затем выбирают на плоскости систему координат и откладывают на оси Х границы разрядов: 130, 170, 210, … На каждом участке оси Х из отрезков длины 40, как на основании, строят прямоугольник высотой .

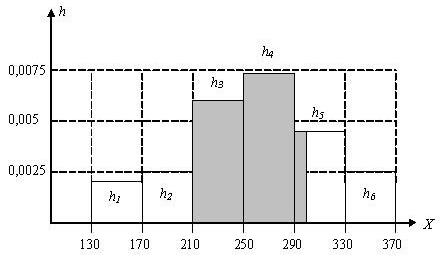
В каждом прямоугольнике площадь равна .

Отсюда правило: чтобы найти долю тех значений Х, которые попадают в некоторый интервал, надо найти площадь той части гистограммы, основанием которой является данный интервал.

Найдем долю значений средних месячных зарплат работников данного предприятия, которые попадают в интервал 210 – 300:

, или 57,5%.

В случае интервального ряда отдельные значения Х не фиксируются, а подсчитываются только абсолютные частоты каждого разряда. Поэтому нельзя использовать формулы (1), (5) и (7) для вычисления , D и S. Однако можно найти приближенные значения этих величин. Для этого находят середины разрядов ; затем вычисляют величины , D и S по следующим формулам:

(8)

(9)

(10)

Результаты расчетов могут быть сведены в таблицу:

Таблица 7.

I
1	150	13,5	- 106,8	11406,24	1026,56
2	190	19,0	- 66,8	4462,24	446,22
3	230	55,2	- 26,8	718,24	172,38
4	270	78,3	13,2	174,24	90,53
5	310	55,8	53,2	2830,24	509,44
6	350	35,0	93,2	8686,24	868,62
		256,8			3113,75

и т. д.

D = 3113,75;

S = .

Интервальный ряд, гистограмма и числовые характеристики, найденные по формулам (8) – (10), составляют математическую модель средней заработной платы на данном предприятии. Она используется при проведении различных социологических исследований, например, при определении уровня жизни работников какой – либо отрасли.

< Предыдущая		Следующая >