24. Векторы и векторные пространства

Первоначально вектором называли направленный отрезок, прикрепленный к одной точке. Для иллюстрации физических величин, имеющих не только величину, но и направление.

Эти величины можно складывать по правилу параллелограмма, вычитать, умножать на числа. При этом, каковы бы ни были векторы И числа Всегда выполняются равенства:

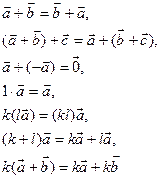( 2)

Позже вектор сделали свободным от точки прикрепления. Свободный вектор - совокупность всевозможных направленных отрезков, параллельных между собой, имеющих одну и ту же длину и одно и тоже направление. Такие отрезки называются эквивалентными. Свободные векторы задаются с помощью координат, т. е. проекций на координатные оси X и Y. В пространстве направленный отрезок имеет три координаты – проекции на координатные оси X, Y,Z.

Вектор можно заменить совокупностью координат. На плоскости это пары чисел в пространстве тройки чисел . Сложение векторов и умножение на число заменяется соответствующими действиями над координатами:

Такая точка зрения на векторы оказалась очень плодотворной. Под определение вектора попало много физических и математических объектов. Например, всякое элементарное событие, происходящее в пространстве в точке с координатами (x, y, z) в момент времени t, можно рассматривать как четырехмерный вектор ( x, y, z, t).

Получается пространство событий.

Количество координат вектора называется размерностью.

Векторы одной размерности можно складывать и умножать на числа по тем же правилам, что двумерные и трехмерные. И при любой размерности будут выполняться свойства (2).

Векторным пространством называется всякое множество, для элементов которого определены операции сложения и умножения на числа таким образом, что выполняются свойства (2).

< Предыдущая		Следующая >