23. Кольца и поля

Числовые множества имеют одинаковые алгебраические свойства:

1) 5)

2) 6) (1)

3) 7)

По этим же правилам производятся операции с многочленами, со всеми элементарными функциями, с рядами. В свойствах (1) отражены некоторые общие свойства указанных множеств. Любое множество с такими свойствами называется Кольцом.

Кольцо- Это такое множество, на котором заданы две функции – сложение и умножение – которые должны подчиняться правилам (1), которые называются Аксиомами кольца.

Операция деления в кольце, вообще говорят, отсутствует. Кольца, в которых можно делить на любой элемент, кроме нуля, называются Полями.

Пример. Докажем, что относительность обычных операций сложения и умножения числа вида С рациональными А и B образует поле.

Обозначим это множество чисел через Р. Покажем, что множество Р замкнуто относительно сложения и умножения. Пусть Тогда

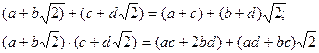
Числа в скобках тоже являются рациональными числами. Проверим деление:

В скобках – рациональные числа, причем знаменатель в поле рациональных чисел в нуль не обращается , следовательно, множество Р – поле.

Пример. Все целые числа разделим на 6 частей: , которые называются Классами вычетов по модулю 6. Из чисел, кратных 6, Из чисел, дающих при делении на 6 единицу в остатке, Из чисел, дающих при делении на 6 двойку остатка, и т. д. Произвольное число класса

Можно записать в виде

Сложение классов определим формулой:

Если

Например,

Умножение определим так: Где M – остаток от деления K×L на 6.

Классы вычетов по модулю 6 образуют кольцо относительно введенных операций сложения и умножения:

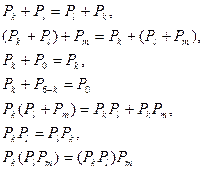
Здесь кольцо построено всего из шести элементов, обозначающих . Можно построить аналогично кольцо по любому модулю Содержащему всего M элементов.

Являются ли кольца вычетов полями? Попробуем разделить На В кольце Пусть , тогда Согласно определению

При любом X имеем Частного Не существует, следовательно, кольцо Не является полем.

Однако таким же способом можно показать, что кольца будут полями. Общий результат формулируется так: кольцо Является полем тогда и только тогда, когда Простое число.

< Предыдущая		Следующая >