21. Интеграл
Различают Определенный и Неопределенный интеграл. Процедура нахождения производной по заданной функции называется Дифференцированием, а обратная процедура, позволяющая находить по заданной производной исходную функцию, называется Интегрированием. Результат интегрирования называется Первообразной Функцией. Поскольку производная от постоянной равна нулю, то
![]() ,
,
Где С – любое действительное число. Поэтому, если для заданной функции F(X) существует одна первообразная F(X), то их существует бесконечно много: F(X) + C. Совокупность всех первообразных заданной функции F(X) называется Неопределенным Интегралом и обозначается ![]() . Например:
. Например:
![]() , т. к.
, т. к. 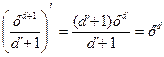 .
.
![]() , т. к.
, т. к. ![]() и т. д.
и т. д.
Присутствующая всюду постоянная С называется Постоянной Интегрирования.
Простейшее применение определенного интеграла – вычисление площади под кривой.
Чтобы найти S, разобьем отрезок [A,B] на маленькие отрезки длиной H.
Верхняя граница заштрихованной фигуры находится между отрезками MN и PQ.
![]()
Такие неравенства запишем для каждого из отрезков длины H, на которые разбит отрезок [A,B], а затем все такие неравенства сложим. Получим неравенства:
![]()
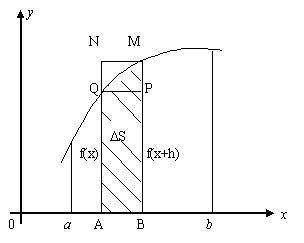 |
S1 и S2 являются функциями от H. Если H неограниченно уменьшать ![]() , то S1 будет увеличиваться, а S2 - уменьшаться. Обе суммы имеют своим общим пределом число S - площадь фигуры.
, то S1 будет увеличиваться, а S2 - уменьшаться. Обе суммы имеют своим общим пределом число S - площадь фигуры.
Площадь получается как предел ![]() или
или ![]() , который называется определенным интегралом и обозначается
, который называется определенным интегралом и обозначается
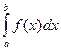 . Связь между определенным и неопределенным интегралами устанавливается формулой Ньютона – Лейбница:
. Связь между определенным и неопределенным интегралами устанавливается формулой Ньютона – Лейбница:
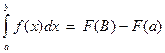 ,
,
Где через F(X) обозначена первообразная функции F(X).
Пример. Площадь под параболой ![]() . Здесь А = 0, B = 1, поэтому
. Здесь А = 0, B = 1, поэтому
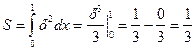 .
.
| < Предыдущая | Следующая > |
|---|