20. Производная
Производная функции F(X) в точке Х представляет собой следующий предел:
![]()
В числителе стоит приращение функции на отрезке [X, X+H].
Физический смысл производной: если рассмотреть функцию пути тела – s(t), то её производная представляет собой мгновенную скорость тела, т. е.
![]()
Производные от некоторых функций:
1. Производная от постоянной функции равна нулю, т. к., если функция не меняется, то её приращение равно нулю: F(X+H) – F(X) = 0/
2. Производная степенной функции ![]() :
:
По определению ![]() . По формуле бинома Ньютона:
. По формуле бинома Ньютона:
![]() .
.
Вычтем ХN, поделим почленно на H и запишем предел суммы как сумму пределов:
![]()
Все пределы, кроме первого, равны нулю, поэтому:
![]()
Правило применимо и для отрицательных степеней.
3. Производная синуса:
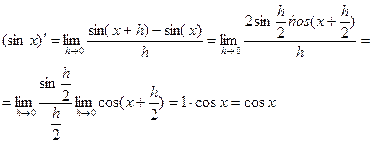
Аналогично доказывается, что ![]() .
.
4. Производная от показательной функции У=Ах:
![]()
При А = Е получаем ![]() .
.
5. Производная от логарифмической функции ![]() :
:
![]()
При А = Е получаем ![]() .
.
При вычислении производных пользуются следующими правилами, которые выводятся с помощью правил вычисления пределов:
![]() ,
,
![]()
Производная от сложной функции F(U(X)) вычисляется по формуле:
![]()
Например:
![]() ;
;
![]()
Приложения производной очень широкие.
Производная от пути – это скорость. Производная скорости – ускорение, т. е. скорость изменения скорости. Задачи на нахождение наибольших и наименьших (экстремальных) значений заключаются в следующем: если непрерывная функция принимает в некоторой точке экстремальное значение и производная в этой точке существует, то производная в этой точке равна нулю.
Пример. В тюрьме строят железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры не менее 2,5 м, а площадь – не менее 6 м2?
Решение. Количество железа пропорционально площади поверхности камеры – параллелепипеда. Пол и потолок имеют площадь Ab каждый, две боковые стены по 2,5А, две другие стены – по 2,5 B. Тогда площадь равна S = 2Ab + 5A + 5B. При этом Ab = 6 (B = 6/A). Следовательно, S = 2×6 + 5(А + B) = 12 + (А + 6/А). Величину А можно выбирать произвольно, она является переменной. Для минимизации функции S(A) следует приравнять нулю S’(A):
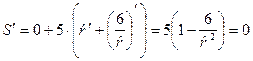
Отсюда ![]() , следовательно,
, следовательно, ![]() . При этом S будет наименьшей. Она равна
. При этом S будет наименьшей. Она равна ![]() (м2).
(м2).
| < Предыдущая | Следующая > |
|---|