18. Предел функции
Начнем с рассмотрения понятия непрерывности функции. В качестве примера возьмем функцию Y = F(X) =X2. Значение функции в точке 2, т. е. f(2) = 22 =4. Рассмотрим на оси Х бесконечную последовательность точек с координатами: Х1 = 2 – 1 = 1; Х2 = 2 – ½ = 3/2; х3 = 2 – ¼ = 1 ¾; … Любое из этих чисел меньше двух. Эти точки скапливаются около точки Х0 = 2.

Разности Х0 – ХK, K>0 уменьшаются в 2 раза и могут стать меньше любого наперед заданного малого положительного числа. Поэтому говорят, что последовательность Х1, Х2, Х3, … стремится к числу 2 или имеет своим пределом число2. при этом функция ведет себя так:
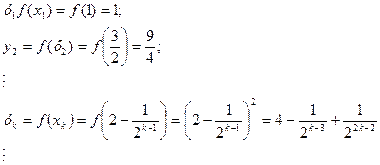
Это бесконечная последовательность. С увеличением K дроби стремятся к нулю, поэтому Yk стремится к четырем:
![]() ,
,
Lim – от латинского limes т. е. граница.
Можно взять другую последовательность: 2 – 1; 2 – 1/10; 2 – 1/100 и т. д.
Она также имеет своим пределом число 2. Таких последовательностей можно указать сколько угодно. Зависит ли предел функции от выбора последовательности, т. е. от того, каким образом переменная Х стремится к двум? Нет, не зависит. Строгое определение предела функции включает в себя требование независимости от выбора последовательности.
Когда предел функции в точке Х0 равен значению функции в этой точке, говорят, что функция Непрерывна в этой точке.
Рассмотрим предел:
![]()
Здесь и числитель, и знаменатель при Х = 1 обращаются в нуль. Поэтому нельзя найти предел, просто подставив единицу. Выполним преобразование:
![]()
Получили новую функцию G(X) = X – 2, где х может принимать любые значения. Во всех точках, кроме х = 1, выполняется тождество F(X) º G(X). График функции G(X) – это прямая. Функция F(X) в точке Х = 1 не является непрерывной. График - тоже прямая, но без точки (1; - 1). Поэтому
![]()
| < Предыдущая | Следующая > |
|---|