17. Корреляционная зависимость

Рассмотрим пример. Между ростом и весом человека существует определенная зависимость. Однако много людей с одинаковым ростом имеют разный вес. Такая зависимость не является функциональной, поскольку для функций каждому Х соответствует единственное значение У.

Можно предположить, что вес зависит не только от роста, но и от размера талии и прочих параметров, но она является очень сложной и пока никем не обнаружена. Можно считать, что вес человека зависит от ряда случайных величин, среди которых рост является одной из основных. Эту зависимость описывают с помощью понятия вероятности. Зависимости такого рода называются стохастическими, вероятностными или статистическими. Важнейшим видом здесь является Корреляционная зависимость.

Рассмотрим в качестве примера вес и рост двадцати курсантов школы МВД:

Номер	1	2	3	4	5	6	7	8	9	10
Рост	178	170	181	173	169	178	177	165	187	182
Вес	72	65	92	75	68	79	78	67	80	81

Номер	11	12	13	14	15	16	17	18	19	20
Рост	159	182	178	173	176	173	198	187	191	170
Вес	56	82	77	63	80	65	85	89	87	72

Изобразим точки графически:

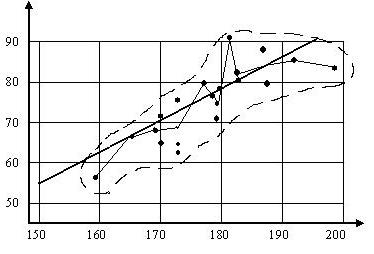Точки лежат внутри некоторой области, или «облака». Заметно, что облако вытянуто вдоль какой – то наклонной прямой. Это означает, что Х и Y Хорошо коррелированы, т. е. при увеличении роста вес, как правило, тоже увеличивается. Соединим точки отрезками, получим Эмпирическую ломаную регрессии. При большем числе измерений эта ломаная больше похожа на прямую.

Прямая, к которой стремится ломаная, называется Регрессией. Она является наилучшим решением задачи построения прямой, относительно которой сумма квадратов вертикальных отклонений экспериментальных точек будет наименьшей. Это задача Метода наименьших квадратов.

Уравнение искомой прямой имеет вид:

,

Где .

Здесь - средние значения роста, веса и их попарных произведений, - дисперсия роста.

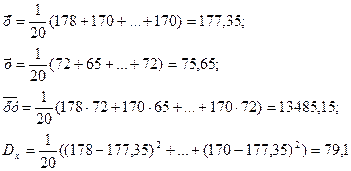
Подставим в формулы, получим:

Получим уравнение прямой:

Это Эмпирическое уравнение регрессии.

Величина R, определяемая по формуле:

,

Называется коэффициентом корреляции. Здесь , , , .

Отсюда

.

Свойства коэффициента корреляции:

1. .

2. Если величины Х и Y независимы, то коэффициент корреляции равен нулю.

3. Если Х и Y связаны линейной зависимостью, то R = 1 или R = - 1, и наоборот.

При совместном изучении двух случайных величин Х и Y прежде всего находят величину коэффициента корреляции, и если он оказывается близким к единице, то имеет смысл описывать корреляционную связь.

< Предыдущая		Следующая >