13. Линейная и постоянная функции
Общепринятая форма записи произвольной линейной функции такова:
![]() , (1)
, (1)
Где K и B – некоторые постоянные, а Х и У – переменные, причем У зависит от Х, т. е. является функцией переменной Х.
Символом Х обозначен произвольный элемент некоторого числового множества, которое называется Областью определения функции.
 |
С помощью системы координат каждую функцию можно изобразить наглядно в виде графика.
Соотношение (1) называется Уравнением построенной прямой, K - угловой коэффициент, ![]() , a - угол между осью Х и прямой.
, a - угол между осью Х и прямой.
Если принять K = 0, то уравнение (1) примет вид:
У = B (2)
Это постоянная функция; она принимает одно и то же значение при любом Х, т. е. не зависит от переменной Х.
 |
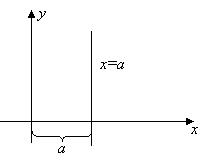
Уравнение
Х = а (3)
Тоже задает постоянную функцию, но здесь Х не зависит от У.
 |
Если У не зависит от Х, то и Х не зависит от У. Х всегда можно выразить через У. В уравнении (1) это будет выглядеть так:
![]() (4)
(4)
Эта функция называется Обратной.
Уравнения (1), (2), (3) можно записать в единообразной форме:
Ах+Ву+С=0, (5)
Где А, В, С – постоянные, причем А и В не могут быть нулями одновременно. В левой части (5) находится многочлен первой степени относительно Х и У. Уравнение (5) называется Общим уравнением прямой.
Рассмотрим изображение функции ![]() и обратной к ней на одном чертеже. В обоих случаях независимую переменную необходимо обозначить одинаково, т. е. Х. Тогда
и обратной к ней на одном чертеже. В обоих случаях независимую переменную необходимо обозначить одинаково, т. е. Х. Тогда
![]() (6)
(6)
 |
Здесь произведена замена
| < Предыдущая | Следующая > |
|---|