40. Критерий знаков для анализа парных повторных наблюдений

Назначение. Критерий знаков используется для проверки гипотезы об однородности наблюдений внутри каждой пары (иногда говорят — для проверки гипотезы об отсутствии эффекта обработки).

Данные. Рассмотрим совокупность случайных пар объема П. Введем величины

Допущения. 1. Все предполагаются взаимно независимыми. Заметим, что мы не требуем независимости между элементами и с одинаковым номером I. Это весьма важно на практике, когда наблюдения делаются для одного объекта и тем самым могут быть зависимы.

2. Все Zi имеют равные нулю медианы, т. е. . Подчеркнем, что законы распределения разных Zi могут не совпадать.

Гипотеза. Утверждение об отсутствии эффекта обработки для повторных парных наблюдений можно записать в виде для всех I= 1,..., N.

Метод. 1. Перейдем от повторных парных наблюдений к величинам , I= 1,..., N, введенным выше.

2. К совокупности , I= 1,..., N применим критерий знаков для проверки гипотезы о равенстве нулю медиан распределений величин , I= 1,..., N (см. п. 4.2).

Приближение для больших совокупностей. Следует воспользоваться нормальной аппроксимацией биномиального распределения.

Связанные данные. Если среди значений есть нулевые, то их следует отбросить и соответственно уменьшить N до числа ненулевых значений .

Оценка эффекта обработки. Нередко для рассматривают модель , , где — ненаблюдаемые случайные величины, Q — некоторая константа, характеризующая положение одного распределения относительно другого (скажем, до воздействия и после). Эту константу часто именуют эффектом обработки. Принятые выше допущения 1 и 2 переносятся на величины . Гипотеза однородности формулируется в виде гипотезы о нулевом эффекте обработки

Введенные величины Q и представления оказываются полезными, если в ходе проверки гипотезы выясняется, что и что поэтому надо оценить количественно то различие, которое привносит обработка (воздействие).

Пример. Покажем как использовать критерий знаков для анализа данных о времени реакции на звук и на свет. В этом примере рассматривается группа испытуемых, а целью исследования служит проверка гипотезы о равенстве времени реакций на звук и на свет. Порядок организации эксперимента позволяет предположить, что полученные данные на одном испытуемом независимы от аналогичных данных для остальных.

Осуществим переход от пар к величинам , I= 1,..., N и запишем последние в виде: , .

Выполняются ли для сформулированной задачи допущения, используемые в критерии знаков? Независимость обеспечивается условиями организации эксперимента. Априорно предполагаемая непрерывность распределений рассматриваемых выборок обеспечивает непрерывность распределения . В случае совпадения распределений времени реакции на звук и на свет справедливо следующее соотношение . Следовательно, , то есть медиана распределения равна нулю. Таким образом, предположение обеспечивает выполнение допущения 2.

Одной из разумных альтернатив нулевой гипотезе в данном случае является предположение о том, что . Далее мы будем использовать критерий знаков против этой односторонней альтернативы.

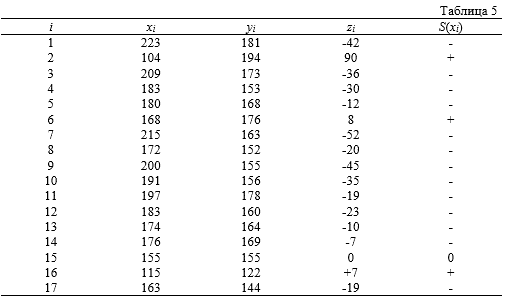
В табл. 5 приведены соответствующие расчеты для данного примера.

Обозначим число положительных значений через . Из таблицы 5 видно, что равно трем, а среди есть одно значение, равное 0. В таких случаях необходимо уменьшить число наблюдений на число значений , равных 0, т. е. перейти от П = 17 к П = 16.

Вычислим вероятность . Для этого воспользуемся таблицами биномиального распределения при , П = 16. Учитывая, что в силу симметрии при , получаем:

То есть минимальный уровень значимости, на котором можно отвергнуть гипотезу о том, что против односторонних альтернатив, равен 0.0106. Учитывая малость этого числа, заключаем, что гипотезу следует отвергнуть в пользу альтернативы .

Обсуждение. Одно из главных достоинств критерия знаков — его простота. Другой важной особенностью этого критерия являются скромные требования к первоначальному статистическому материалу. Эти требования описываются с помощью модели парных наблюдений.

< Предыдущая		Следующая >