10. Интегральная теорема Лапласа

Мы видели, что отыскание вероятности появления события А при П испытаниях, количество которых заключено в границах целых чисел А и B, было связано с применением теоремы сложения вероятностей. Именно, если Т принимает значения всех последовательных целых чисел , где и То вероятность того, что событие А наступит либо раз, либо раз, ..., либо раз, т. е. вероятность появления события А при П испытаниях не менее А И не более B раз, определяется по формуле

Отыскание этой суммы с помощью данных биномиального распределения по мере возрастания числа П сопровождается значительными затруднениями вычислительного характера. Между тем такая задача может быть успешно разрешена приближенно и притом с желательной степенью точности на основании интегральной теоремы Лапласа.

Теорема. Если производится большое число п независимых испытаний, в каждом из которых вероятность наступления события А равна р, то вероятность того, что число т появлений события А удовлетворяет неравенству

Имеет своим пределом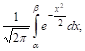

Когда п неограниченно возрастает.

Математическая запись этой теоремы:

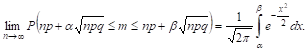
Доказательство. Пусть число П независимых испытаний зафиксировано. Тогда принятые в условии границы значений M — определенные целые числа.

Обозначив их через А и B, будем иметь:

и .

Искомая вероятноСтЬ в указанных границах числа Т Определяется СОгЛАсно теореме сложения вероятностей

При этом значения слагаемых вычисляются либо (для нЕбОльших П и Т) по формуле Бернулли, либо по формуле Лапласа.

Отыскание же предела, к которому стремится вероятность

При неограниченном возрастании числа П, может быть осуществлено только с помощью определенного интеграла.

Приведем поэтому выражение К виду интегральной суммы.

Общий член суммирования

Мы можем представить, пользуясь асимптотической формулой биномиального расПределения, в виде

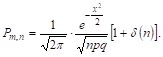
Здесь при для всех целых Т в заданных границах. Но переход к переменной Х связан с выделением в общем члене суммирования множителя и с установлением граНИц для переменной Х.

При рассмотрении асимптотической формулы было принято соотношение

(1)

Это соотношение приводит в соответствие числу значение , числу - значение и т. Д.

Так как паре последовательных чисел M и Т +1 соответствует пара значений X И , то имеем два соотношения:

и

Отсюда вычитанием находим

А это показывает, что условие непосредственно влечет за собой условие

Таким образом, общий член интегральной суммы может быть записан в виде

(здесь вместе с ).

Границы значений переменной Х определяются из условия теоремы о границах числа Т. В самом деле, переписав сООтношение (1) в виде

Можно на основании нЕРавенстВ

Установить, что значения Х заключены в границах чисел A и B, т. е.

При фиксированном П имеем интегральную сумму

Которая с изменением П является переменной величиной.

Переход к пределу (для левой части при , а для правой Части при ) обращает в нуль второе слагаемое в правой части, и отсюда

Полученное равенство можно переписать в соответствии с формулировкой рассмотренной теоремы:

Дадим геометрическое истолкование теоремы. Чтобы графически представить преобразованный общий член ИнТегральной суммы , обратимся к кривой, соответствующей функции (рис. 4).

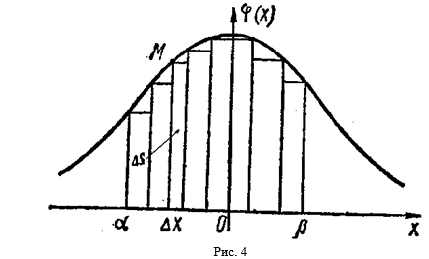
Если М — произвольная точка на этой кривой, то произведению будет СоотВетствовать площадь прямоугольника с высотой, равной ординате точки М [это — значение функции ], и с основанием, равным элементарному отрезку на оси Ох, соответствующему в силу соотношения (1) приращению на 1 числа M появлений события А.

Интегральная сумма, выражающая приближенное значение искомой вероятности, численно равна площади ступенчатой фигуры, составленной из элементарных прямоугольников в заданных границах между A и B.

Полученный определенный интеграл, дающий предельное значение той же вероятности при , численно равен площади криволинейной трапеции, ограниченной сверху кривоЙ

,

Снизу осью Ох и с боков перпендикулярами к оси Ох в точках и .

До перехода к применению полученного результата при вычислении вероятностей рассмотрим частный случай, когда число Т принимает все возможные значения от 0 до П, т. е. когда ищется

Так как условие связано с достоверностью события, то

И это сохраняется при неограниченном возрастании числа независимых испытаний, т. Е. и

Найдем пределы соответствующего этому случаю интеграла, т. е. границы значений переменной Х.

Из соотношения (1) можно установить, что при а из следует ; при а из следует .

Отсюда

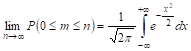
И, таким образом,

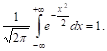
Из установленной сходимости этого интеграла (его называют интеграЛОм Лапласа) непосредственно следует, что

А отсюда легко перейти и к интегралу Пуассона.

Действительно, замена дает

и

Поэтому

Интегральная теорема Лапласа применяется для вычисления вероятности того, что число Т появлений события А заключено в фиксированных границах

При заданном числе испытаний. Поэтому соответствующая формула приобретает уже приближенный характер, т. е.

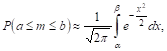
И точность достигаемого результата повышается с возрастанием количества испытаний.

Самое отыскание вероятностей связано с определением численных значений найденного интеграла Лапласа

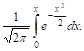
При этом для непосредственных вычислений принята специальная функция, представляющая удвоенный интеграл Лапласа, т. е. Функция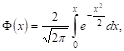

Значения которой находятся, например, с помощью степенных рядов.

Эта функция имеет следующие два свойства:

1) с возрастанием Х значения Ф(Х) возрастают, приближаясь к единице;

2) так как ряд, представляющий эту функцию, состоит из нечетных степеней Х, то , т. е. эта функция нечетная. Численные значения функции Ф(Х) даются в специальной таблице, и это позволяет находить интеграл

По следующей формуле:

Справедливость этой формулы может быть установлена учащимся.

Таким образом, вся операция состоит в отыскании значений A и B, соответствующих границам А и B, с последующим обращением к табличным значениям и , и в использовании формулы

Пример 13. Вероятность попадания в цель из скорострельного орудия равна при отдельном выстреле 0,8. Найти вероятность того, что число попаданий при 900 выстрелах будет заключено в гранИЦах чисел 690 и 740.

Решение. Здесь N = 900,

Соотношения

и

Здесь дают:

И

Отсюда

Искомая вероятность

Пример 14. При вытачивании болтов наблюдается в среднем 10% брака. Можно ли быть уверенным, что в партии из 400 болтов окажутся пригодными более 299?

Решение. Принимая Р = 0,9, будем искать .

Значения A И B определим из соотношений:

И

Отсюда

И

Таким образом,

Но оба значения Ф(Х) выходят из границ таблИЦы, которая составлена для значений Х не свыше 4,50. Значениям же Х > 4,50 соответствуют значения Ф(Х), мало отличающиеся от 1, и поэтому искомая вероятность практически принимается равной 1.

Это означает, что наличие в данной партии более 299 пригодных болтов можно считать достоверным.

Следует заметить, что формула для вычисления вероятности по теореме Лапласа несколько упрощается в случаях, когда границы А И B для возможного числа появлений события А симметричны относительно числа Пр, т. е.

И

Тогда

Пример 15. Пусть при , Р=0,8 и Q=0,2 требуется найти

Решение. Здесь и поэтому значение A можно найти из соотношения где и .

Значит , а отсюда

Использование функции Ф(Х) позволяет также ответить на вопрос о вероятности того, что отклонение частости события () от его вероятности в отдельном ИСпытании (P) не превысит заданной величины. Такой результат достигается следующим преобразованием неравенств (в теореме Лапласа).

Деление всех членов неравенств на П дает:

Эти неравенства эквивалентны неравенствам:

Если абсолютная величина отклонения то , и тогда в силу сохранения вероятности выполнения эквивалентных неравенств имеет место соотношение

Или

Переход к заданной величине отклонения E дает

Этот результат позволяет с помощью функции Ф(Х) установить вероятность того, что отклонение частости события при П Испытаниях от его вероятности по абсолютной величине не превышаЯ Заданного числа E.

Пример 16. Вероятность появления события А в отдельном Испытании Р=0,6. Найти вероятность того, что при 150 испытаниях частость появления этого события будет отличаться от его Вероятности не более чем на 0,03.

Решение. Здесь надо искать при условиях , , и Так как

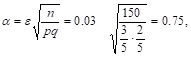
То

Упражнения.

1. В партии деталей двух сходных форматов число крупных деталей вдвое больше числа мелких. Детали сложены без всякого порядка. Какова вероятностЬ Того, что среди взятых наудачу 10 деталей окажется 6 крупных?

Ответ:

2. ВероятНОсть поражения мишени при каждом отдельном выстреле Р=0,8. Найти вероятность того, что при 5 выстрелах мишень будет поражена.

Ответ:

3. В хлопке имеется 10% коротких волокон. Какова вероятность того, чтО В наудачу взятом пучке из пяти волокон окажется не более двух коротких?

Ответ:

< Предыдущая		Следующая >