09. Асимптотическая формула биномиального распределения (локальная теРЕма Лапласа). Формула Пуассона

Уже для двузначного числа П повторных испытаний определение вероятности по формуле Бернулли

вызывает вычислительные трудности. Поэтому в таких случаях применяется следующая приближенная формула:

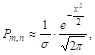
Выражающая содержание Локальной теоремы Лапласа, вывод котоРОй в настоящем курсе опускается (желающие ознакомиться с этой теоремой могут найти ее в подробных курсах теории вероятностей).

Здесь

При этом пользуются табличными данными для второго множителя в правой части формулы

Для возможности выполнения вычислений с помощью асимптотической формулы в справочниках дана соответствующая таблица значений .

Для того чтобы показать, сколь незначительно отклонение результата применения приближенной (асимптотической) формулы при вычислении РТ,п От результата вычисления по точной формуле, проведем оба вычисления на следующем примере.

Пример 11. ВероятноСть попадания по движущейся мишени принимается равной 0,7. Какова вероятность того, что из 20 выстрелов 15 окажутся удачными?

Решение. Здесь П=20, и Q=0,3. Производим вычисление по приближенной формуле.

I. Определяем

II. Определяем

III. Определяем значение

IV. Определяем

Вычисление по точной формуле биномиального распределенИЯ:

Логарифмирование дает нам

Отсюда И, таким образом, приближенный результат, найденный выше, дает отклонение на 3,35%. С повышением значения П этот процент понижается.

Пусть в условиях предыдущего примера требуется найти вероятность того, что 5 выстрелов окажутся удачными.

Обращение к формуле Бернулли дает

(промежуточные операции по подсчету результата отнесены к самостоятельной работе учащегося).

Столь незначительное значение найденной вероятности указывает на то, что ожидаемое событие является практически невозможным. Применение приближенной формулы Лапласа дает:

По таблице значений не может быть найдено, так как в таблице приведены значения для значений не свыше 3,99. Значениям же Х > 3,99 соответствуют ничтожно малые значения , что указывает на практическую невозможность события.

График функции называют Кривой Вероятно Стей.

Несложное исследование функции дает следующее.

1. Так как здесь Х входит в четной степени, то , т. е. соответствующая этой функции кривая симметрична относительно оси Оу.

2. С осью Оу кривая пересекается в точке .

3. С осью Ох кривая не пересекается, так как показательная функция при всех действительных значениях Х; при этом ось Ох является горизонтальной асимптотой для кривой, так как

4. Производная исследуемой функции

Обращается в нуль при Х = 0, причем переход через нулевое значение связан с переменой знака производной с «+» (при Х < 0) на «-» (при Х > 0); этим в точке определяется максимум функции, равный

5. Вторая производная обращается в нуль при и с переменой ее знака, когда Х переходит через — 1 и через 1, а этим, как известно, определяются точки перегиба

Ординаты этих точек

6. Составляем таблицу для ряда значений Х и и вычерчиваем кривую (рис. 3).

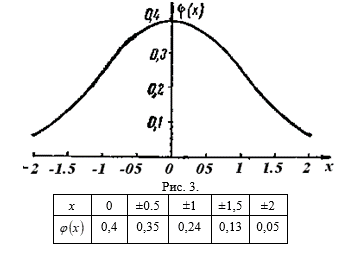
Построенная кривая и есть кривая вероятностей. Она позволяет по каждому значению найти приближенное значение

А отсюда и

Асимптотическая формула 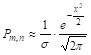, выражающее содержание локальной теоремы Лапласа, дает тем более близкие к точному значению Рт, п результаты, чем больше значение При этом, здесь сказывается не только значение П, но и значение Pq. При одних И Тех же значениях П вычисление по асимптотической формуле дает длЯ Рт, п тем лучшее приближение к значению по формуле Бернулли, чеК Ближе Pq к 0,25 (это значение является для Pq наибольшим), т. Е. чеМ Заданная вероятность (а отсюда и Q) ближе к 0,5. В задачах же со Значениями Р или Q, близкими к нулю, применение той же асимптотической формулы дает более заметные отклонения от точных Значений Рт, п, получаемых по формуле Бернулли.

Так, в примере 11 при П=20, M=15 и Р=0,7 приБлиженный результат дает отклонение на 3,35%. Если же, не меняя значений П И Т, положить Р=0,95 (Q=0,05), то значению по формуле Бернулли соответствует по формуле Лапласа значение , что указывает уже на непригодность этой приближенной формулы.

В связи с этим для так называемых Редких событий (со значениями Р, близкими к нулю) с успехом применяется асимптотическая формула Пуассона в виде

Где и приближение тем лучше, чем больше П и меньше Р. Заметим, что использование этой формулы допустимо при условии

Выгодность применения вычислений по формуле Пуассона, например, для П=100 и Р= 0,01, показывает следующая таблица значений

При значениях Т 0 1 2 5 9

По формуле Бернулли 0,366 0,370 0,185 0,003 0,000001

» Лапласа 0,242 0,411 0,242 0,001 0,000000

» Пуассона 0,368 0,368 0,184 0,003 0,000001

Пример 12. Известно, что в прИНятой для сборки партии из 1000 деталей имеются 4 дефектных. Найти вероятность того, что среди 50 наудачу взятых деталей нет дефектных. ]

Решение. Здесь П = 50, вероятность появления дефектной детали Р = 0,004, вероятность появления пригодной детали Q = 0,996. Отсутствие среди 50 деталей дефектных, означает, что все эти детали — пригодные. Поэтому при Т=0 обращение к формуле Бернулли дает . Логарифмированием находим L, откуда

Для применения формулы Пуассона имеем

Отсюда

Что дает отклонение от результата по формуле Бернулли менее 0,5%. Заметим, что обращение к приближенной формуле Лапласа требует более громоздкого вычисления и дает , т. е. с отклонением около 1,7%.

< Предыдущая		Следующая >