67. Общая характеристика задач динамического программирования и их геометрическая и экономическая интерпретации

В рассмотренных выше задачах линейного и нелинейного программирования мы находили их решение как бы в один этап или за один шаг. Такие задачи получили название одноэтапных или одношаговых.

В отличие от этих задач задачи динамического программирования являются многоэтапными или многошаговыми. Иными словами, нахождение решения конкретных задач методами динамического программирования включает несколько этапов или шагов, на каждом из которых определяется решение некоторой частной задачи, обусловленной исходной. Поэтому термин «динамическое программирование» не столько определяет особый тип задач, сколько характеризует методы нахождения решения отдельных классов задач математического программирования, которые могут относиться к задачам как линейного, так и нелинейного программирования. Несмотря на это, целесообразно дать общую постановку задачи динамического программирования и определить единый подход к ее решению.

Предположим, что данная физическая система S находится в некотором начальном состоянии и является управляемой. Таким образом, благодаря осуществлению некоторого управления U указанная система переходит из начального состояния S0 в конечное состояние При этом качество каждого из реализуемых управлений U характеризуется соответствующим значением функции W(U). Задача состоит в том, чтобы из множества возможных управлений U найти такое U*, при котором функция W(U) принимает экстремальное (максимальное или минимальное) значение W(U*). Сформулированная задача и является общей задачей динамического программирования.

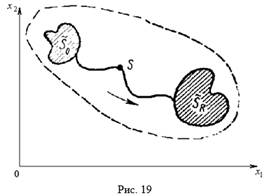
Дадим геометрическую интерпретацию этой задачи. Предположим, что состояние системы характеризуется некоторой точкой S на плоскости X1Ox2 (рис. 19) и эта точка благодаря осуществляемому управлению ее движением перемещается вдоль линии, изображенной на рис. 19, из области возможных начальных состояний в область допустимых конечных состояний . Каждому управлению U движением точки, т. е. каждой траектории движения точки, поставим в соответствие значение некоторой функции W(U) (например, длину пути, пройденного точкой под воздействием данного управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий движения точки S найти такую, которая получается в результате реализации управления U*, обеспечивающего экстремальное значение функции W(U*). К определению такой «траектории» сводится и задача динамического программирования в случае, когда допустимые состояния системы S определяются точками N-мерного пространства.

Экономическую интерпретацию общей задачи динамического программирования рассмотрим на конкретных примерах.

1.30. В распоряжение министерства, в подчинении которого находится K предприятий, выделены средства в размере К Тыс. руб. для использования их на развитие предприятий в течение Т лет. Эти средства в начале каждого хозяйственного года (т. е. в моменты ) распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная ими за прошедший год прибыль. Таким образом, в начале каждого I-го года рассматриваемого периода J-е предприятие получает в свое распоряжение тыс. руб. Задача состоит в определении таких значений , т. е. в нахождении таких распределений выделенных средств между предприятиями и получаемой ими прибыли, при которых за Т лет обеспечивается получение максимальной прибыли всеми предприятиями.

Сформулировать поставленную задачу в терминах общей задачи динамического программирования.

Решение. Предполагая, что J-му предприятию на I-Й год выделяется тыс. руб., будем рассматривать данное распределение средств как реализацию некоторого управления . Таким образом, управление состоит в том, что на I-м шаге первому предприятию выделяется тыс. руб., второму тыс. руб. и т. д. Совокупность чисел определяет всю совокупность управлений на Т шагах распределения средств как Т Точек в K-мерном пространстве.

В качестве критерия оценки качества выбранного распределения средств, т. е. реализуемых управлений, взята суммарная прибыль за Т лет, которая зависит от всей совокупности управлений:

Следовательно, задача состоит в выборе таких управлений т. е. в таком распределении средств, при котором функция W принимает максимальное значение.

Как видно, сформулированная задача является многоэтапной. Эта многоэтапность определяется ее условиями, которыми предусмотрено принятие определенных решений в начале каждого года рассматриваемого периода времени. Вместе с тем в целом ряде других задач динамического программирования такая многоэтапность непосредственно не следует из их условий. Однако в целях нахождения решения такие задачи целесообразно рассматривать как многоэтапные. Приведем пример подобной задачи и дадим ее формулировку в терминах общей задачи динамического программирования.

1.31. Для увеличения объемов выпуска пользующейся повышенным спросом продукции, изготовляемой предприятиями, выделены капиталовложения в объеме S тыс. руб. Использование I-М предприятием тыс. руб. из указанных средств обеспечивает прирост выпуска продукции, определяемый значением нелинейной функции

Найти распределение капиталовложений между предприятиями, обеспечивающее максимальное увеличение выпуска продукции.

Решение. Математическая постановка задачи состоит в определении наибольшего значения функции

(1)

При условиях

(2)

(3)

Сформулированная задача является задачей нелинейного программирования. В том случае, когда — выпуклые (или вогнутые) функции, ее решение можно найти, например, методом множителей Лагранжа. Если же функции не являются таковыми, то известные методы нахождения решения задач нелинейного программирования не позволяют определить глобальный максимум функции (1). Тогда решение задачи (1) - (3) можно найти с помощью динамического программирования. Для этого исходную задачу нужно рассмотреть как многоэтапную или многошаговую. Вместо того чтобы рассматривать допустимые варианты распределения капиталовложений между П предприятиями и оценивать их эффективность, будем исследовать эффективность вложения средств на одном предприятии, на двух предприятиях и т. д., наконец, на П предприятиях. Таким образом, получим П этапов, на каждом из которых состояние системы (в качестве которой выступают предприятия) описывается объемом средств, подлежащих освоению K предприятиями . Решения об объемах капиталовложений, выделяемых K-му предприятию , и являются управлениями. Задача состоит в выбор таких управлений, при которых функция (1) принимает наибольшее значение.

< Предыдущая		Следующая >